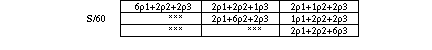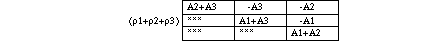SPEEDUP COMPARISON BETWEEN FE AND FD PARALLEL CFD CODES ON CRAY C98
J.P. GREGOIRE, B. THOMAS
D.E.R. Electricité de France
Département MMN
1, avenue du Général de Gaulle
92141 CLAMART CEDEX - FRANCE
jean-pierre.gregoire@der.edfgdf.fr
bernadette.thomas@der.edfgdf.fr
Abstract:
Parallelism appears to be a promising answer to the ever increasing users' demands on maximal computation speed and maximal mesh size in industrial CFD computations. So two CFD codes using the same time solver, N3S, a code based on FEM, and ESTET, a code based on FDM have been parallelized at the Research Center of Electricité de France.
In this paper we compare the parallelization of each code step by step, present the two resulting speed-ups and analyse why they are so different.
Introduction
Two production codes for computational fluid dynamics applications, N3S and ESTET, have been parallelized [3] [4] at EDF's Research Center, on a CRAY C98, under the following constraints :
- no algorithm modification and thus identical binary
- results.
- parallelism introduced only at low level routines.
- sequential and parallel versions merged into a single one.
These codes solve the unsteady thermal turbulent Navier-Stokes equations using the same fractional step method.
The only difference between them lies in the choice of the discretization method : Finite Element Method (FEM) on unstructured meshes for N3S, Finite Difference Method (FDM) on structured grids for ESTET.
The consequences of this choice are well known, more complex calculations with indirect addressing and more memory consumption for N3S than for ESTET.
In the present paper we analyse an other effect of this choice: after parallelization the speedups on 8 processors, almost 3. for N3S and 4.7 for ESTET, are different.
N3S-ESTET algorithms
For a full description of the algorithms, the reader is referred to [1]. Briefly, the unsteady Navier-Stokes equations are averaged in time and the Reynolds tensor is modelized by an eddy viscosity derived from the k-[[epsilon]] model. This averaged equations, which are still unsteady but for a larger time scale, are solved using a fractional step scheme. The different operators involved, i.e., convection, diffusion, pressure-continuity, are solved one after the other rather than all at the same time. The splitting is shown to be first or second order accurate in time according to the user's choice.
Then the bulk of the computation takes place in a time-loop on which the paper focuses. The time-loop consists in four steps as follows :
1) update of the matrices (for eddy viscosity evolution) and right hand sides.
2) solution of the advection step through a characteristics method.
3) solution of the diffusion of the velocity.
4) solution of the projection (Chorin-Temam) step.
The first step consists in Finite Element or Finite Difference calculations. The second step uses a method which is naturally parallel (a Lagrangian method). The third and fourth steps consist actually in the solution of a symmetric positive definite system resulting from the choice of the time and space discretization. They are solved by a preconditioned conjugate gradient algorithm (PCG).
Parallelization strategy
At EDF's Research Center, we have already used the parallelization strategy described above on several codes. The resulting speedups have proved its efficiency.
Using the CRAY tool FLOWTRACE we trace computational time consumption for each time step for a representative test case of each code in the following table:
|
N3S |
ESTET |
|
| update of matrices |
5% |
2% |
| convection |
60% |
36% |
| diffusion of velocities |
8% |
10% |
| projection |
12% |
49% |
| total |
85% |
97% |
These calculations, to be parallelized, are located inside nearly 30 routines for both codes but the resulting theoretical speed-ups are different : 3.9 for N3S code and 6.6 for ESTET code.
The parallelization will be implemented at 3 different levels:
- single DO loop.
- nested DO loops.
- parallelization at high level.
The CRAY parallelizer fpp automatically parallelizes the outer DO loop, selects the scope (private or shared) of each variable and keeps vectorized the inner one.
However we must control this automatic parallelization, for example fpp does not generate private arrays and consequently parallelizes only inner DO loops. The resulting parallelization is very poor. In this case we parallelize by hand by introducing COMPILER DIRECTIVES while data scoping is determined using the CRAY ATSCOPE tool.
This parallelization is introduced without any code modification nevertheless we got a good load balancing and large enough granularity on large meshes.
The parallelization at high level is only introduced in ESTET code inside the routine implementing the characteristics method.
Stability of the the parallel results
As the time-loop presented before has not a strong robustness and as the turbulence model contains some numerical constants adjusted to the sequential results it is important that the parallel binary results be identical to the sequential ones.
Parallelization of matrix calculations
In ESTET code
In the FDM these calculations are very simple : the expressions are explicit, the connection between the grids points are fixed, the matrices have a diagonal structure and no assembling is needed to construct them.
In N3S code
In the FEM the situation is more complex. To simplify these calculations, generaly carried out using numerical integration by GAUSS formulas, we restrict to triangles in 2D and tetrahedrons in 3D. The FE elementary matrices M are in this way computed using precalculated analytical formulas of the form [2] :
where V is the surface in 2D and the volume in 3D of the FE, N a positive integer.
For the mass matrix, the coefficients of the matrix Z are relative integers, which do not dependent on the FE shape as illustrated by tables 1 and 2.
For the Laplacian matrix, the coefficients of the matrix Z are geometric expressions which depend on the FE shape. N and Z depend only on the shape function degree and the space dimension. In 2D the surface S disappears while the volume is present in 3D (see tables 3 and 4).
For both methods these calculations are implemented in a vector DO loop over all the FE or over the grid points. Using compiler directives, the CRAY fpp preprocessor will automaticaly parallelize this DO loop by distributing chunks of vectors on the different processors.
In the FEM, the assembling of the elementary matrices into the global matrix needs to protect the global matrix to avoid vector dependencies. This fact involves a high implementation cost which prevents the parallelization of this operation.
Resulting speed-ups
The parallel efficiency for this step is optimal for ESTET and reaches 0.7 only for N3S.
Parallelization of of the characteristics method
The convection-diffusion equation on [tn,tn+1] can be written as :
where [[phi]] contains the diffusion term and the source term.
By integrating this equation between tn and tn+1 along the characteristics curve XM(t) which is located at the point M at the time tn+1, we get :
This expression is exact in time. In order to get an approximation of C(Xx(tn),tn) we linearize the equation of the curve Xx(t). Then we integrate the differential equation by a Runge-Kutta method.
So we are led to search the origin P of the characteristics curve XM(tn). It gives us the value of C(XM(tn),tn) because the field C is known at tn. If XM(tn) is not a point of the mesh, we get C(XM(tn),tn) by FE interpolation.
As far as the parallelization of this method is concerned, the main point is that the characteristics curve of each mesh node can be processed in parallel.
The CRAY fortran preprocessor, fpp, is unable to parallelize automatically the do loop over the nodes due to its complexity, i.e., 600 source code lines, numerous inner loops and conditional jump instructions. We have to insert by hand CRAY compiler directives to force the parallelization.
These directives need to define the scope of each variable in the parallel region. The CRAY ATSCOPE tool can be used to generate automatically the scope for each variable. The output is not 100% safe because it can be mislead by constructs like backward GOTO statements and has to be rechecked by hand.
For the ESTET code, the simple construction of the characteristics curves allows to implement the parallelization inside the original routine by computing several vector registers of grid points in parallel. The resulting parallelization was very poor and we modify the implementation of the routine as follows :
- we reorder the grids points, eliminate those needing special computation, and collect them in chunks of a multi ple of 128 elements in a pre-treatment.
- we transform the initial routine by a sequence of con- current calls to a new routine devoted to compute in vector mode the characteristic curves of one chunk.
Resulting speed-ups
For both codes we measured a nearly linear speed-up relative to the number of processors and obtained a maximum speed-up of 7. on 8 processors in dedicated mode.
Parallelization of PCG
In N3S code
The PCG is always used with diagonal preconditioning (60 iterations to obtain a relative residual of 1.E-7 for a problem of size 350 000).
So 80% of computing time is consumed by the matrix vector product and the remaining 20% is devoted to the elementary vector operations, i. e., inner products and vector update.
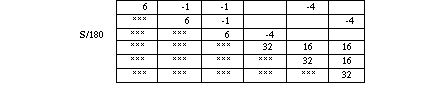
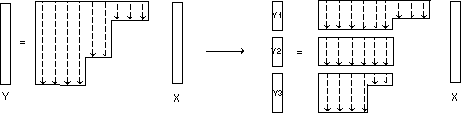
In order to parallelize the sparse matrix-vector product, Y=A*X, originally done using full jagged diagonal matrix format, we divided the matrix into blocks (see table 5).
The number of blocks is specified as a multiple of the number of available processors which depends of the working mode of the computer (dedicated or production mode).
The variable number of rows in each block is determined in such a way that the number of coefficients inside each block remains constant. Therefore the load balancing is good while the vectorization remains efficient.
In this way Y is computed piecewise on each processor. This operation only needs to add to the original matrix structure a few pointers describing the partitioning of Y and of the sub jagged diagonals inside the blocks.
Note that the original matrix format is slightly increased and is contained in the new one when the number of blocks equals 1 . In this way the parallelized and the sequential version of the matrix vector product are implemented in the same kernel.
In ESTET code
The PCG is always used with polynomial preconditioning consuming 40% of computing time. The matrix vector product, implemented inside the PCG, consumes 40%.
The matrix vector product and the polynomial preconditioning use the same matrix. This one is compacted by elimination of rows corresponding to non free unknowns and therefore row addressing becomes indirect.
The parallelization of the matrix vector product is automatically introduced by fpp parallelizer at the level of the DO loop over the free unknowns.
Since the order of the free unknowns in the indirect addressing is arbitrary, we reorder it by the red and black coloring algorithm. Therefore in the polynomial preconditioning, each DO loop over the free unknowns can be splited in 2, one computing the red unknowns using black ones, the other computing the reverse. This trick significantly increases the rate of convergence of PCG while the 2 DO loops remain vectorized by CRAY compiler using the compiler DIRECTIVE "ignore vector dependency".
To parallelize these 2 DO loops we must force fpp parallelizer because for fpp "no vector dependency" does not imply "no parallel dependency". Therefore the parallelization is efficient while the vectorization is preserved.
Resulting speed-ups
In order to reproduce the same binary results in parallel mode as in sequential mode we do not parallelize the inner products. The only optimisation we perform is to compute 2 inner products in the same time. Therefore the degree of parallelism of the PCG is 85%.
The parallel version on the PCG produces identical results to the sequential one and the resulting speedups, in dedicated mode, are presented in the following table:
| NCPUS |
2 |
4 |
6 |
8 |
| N3S speed-up |
1.6 |
2.7 |
3.1 |
3.5 |
| ESTET speed-up |
1.6 |
2.8 |
3.3 |
3.7 |
Timings on CRAY C98 in dedicated mode.
N3S code
The timings are measured on the following test case:
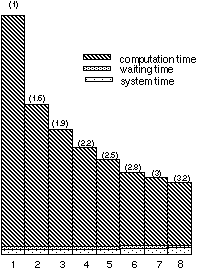
boron mixing in thermal turbulent transient flow in a PWR vessel. The mesh is composed of 360,000 iso-P2 velocity nodes, 60,000 P1 pressure nodes and 240,000 tetrahedrons. The used turbulent model is k-[[epsilon]] model. Velocity, k, [[epsilon]], temperature, passive tracer, boron concentration, pressure are discretized which leads to a total number of about 3000,000 unknowns. The computational time for each time step is 52 seconds and the instationary state of the flow is obtained after 600 time steps in 30 hours of CRAY C98.
Substracting from the global connected time the initialization one (not parallel) and comparing to the CPU time on 1 CPU we obtained the following speed-ups of the parallelized time loop:
The global speedups (shown in parenthesis) are to be compared with the theoretical ones given by the Amdahl's law (1. 7, 2.3, 2.8, 3.1, 3.4, 3.7, 3.9) with 85% of code parallelized.
If we correct this law, by taking into account waiting for I/O and system times which cannot be decreased by parallelization, the new theoretical speedups obtained are close to those measured.
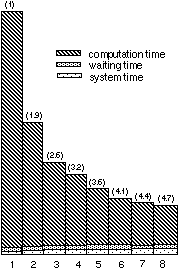
ESTET code
We repeat the same measurements as before on the following test case: computation of the isothermal turbulent flow inside a Stairman cyclone separator of particles. The k-[[epsilon]] turbulence model is used and the grid size is 61*69*89 (374,601 grid points). A passive scalar is added to check the convergence towards the steady state. We obtain the following speed-ups:
Timings on CRAY C98 in production mode.
In the last paragraph we have shown the speed-ups, in dedicated mode, of the parallelized version of both codes.
However, an ordinary execution of them will be done on a non-dedicated machine, and the user has to share the parallel execution with other users, wait for aviable resources and will be eventually swapped and rescheduled.
Depending of the loading of the machine the obtained speed-ups vary in a range between 40% and 90% of the speed-up in dedicated mode on 8 CPUS.
Generally the speed up seems to be close to 2.7 for N3S code and 4. for ESTET code.
Remark on the speed-ups
As the FDM programming is simpler than the FEM one, the computation time is concentrated inside a smaller number of subroutines in ESTET code than in N3S code.
Consequently, after a parallelization effort of same size in both codes, the parallel part is larger for the first code than for the second one and the first resulting theoretical speed-up (3.9) is 1.7 times smaller than the second one (6.6).
After measurements the maximal speed-ups (3.2 and 4.7), on 8 CPUS, are in a lower ratio of 1.4 and the corresponding efficiencies (relative to theoretical speed-ups) are : 0.8 compared to 0.7 .
This difference between the efficiencies is due to the memory acceses during parallel execution. In the FEM using the indirect memory access on compressed sparse arrays, the increase of the memory conflicts inter-CPUS is lower than in FDM where the memory access is regular.
Conclusion
The obtained results are entirely satisfactory from our industrial point of view.
We had put heavy constraints on the parallelism strategy which induced loss of efficiency : the algorithms are preserved, only the inner most routines are modified, the binary results are identical whatever the number of used CPUS, the code keeps its portable status, the runs are done on standard meshes and on loaded machines.
Yet the results are encouraging. The user is now able to perform a study roughly three times faster than before.
Finally an interesting point for the maintenance of the code is that very few routines were modified and an unique version, both sequential and parallel, is kept.
References
[1] GREGOIRE J.P., NITROSSO B., POT G.
Conjugate gradient performances enhanced in the C.F.D. code N3S by using a better vectorization of matrix vector product, Proceedings o IMAC'S 91, Dublin, July 1991.
[2] GREGOIRE J.P., POT G.
Speed-up of CFD codes using analytical FE calculations ,
14 th. Int. Conference on Numerical Methods for Fluids Dynamics, Bangalore, India, July 1994.
[3] J.P. GREGOIRE, B. NITROSSO, Y. SOUFFEZ, G. ROTH.
Speedup ol parallelized N3S code on CRAY C98 in production mode , IX International Conference on FINITE ELEMENTS IN FLUIDS,Venezia October 1995.
[4] J.P. GREGOIRE, J.D. MATTEI, G. SIMEONI .
Parallelization of ESTET code on CRAY C98 , HPCN 97, Vienna April 997.
Table 1 : 2D quadratic mass matrix ( analog in 3D)
Table 2 : 2D linear mass matrix with linear [[rho]] ( analog in 3D)
Table 3 : 2D quadratic Laplacian matrix ( s=A1+A2+A3 )
Table 4 : 2D linear Laplacian matrix with linear [[rho]]
Table 5: parallelization of matrix-vector product