Eduardo Ramos
Energy Research Center
UNAM
62580 Temixco, Mor., MEXICO
erm@servidor.unam.mx
Luis M. de la Cruz and Victor Godoy
Visualization Laboratory, DGSCA
UNAM
04510 México, D.F. MEXICO
lmd@labvis.unam.mx
victor@labvis.unam.mx
lmd@labvis.unam.mx
www.labvis.unam.mx/labvis/
This paper presents a visualization technique which shows the geometric deformation of a fluid moving by natural convection inside a cubic container. The technique is based on intensive numerical calculations and the use of sophisticated visualization tools. The convective motion is produced by maintaining the temperatures of two opposite vertical walls of the container at constant value but different values. All other sides are considered to be thermally insulated. The wall temperatures oscillate as a function of time. Due to the combined effect of time-dependent temperature difference and gravity acceleration, vortices are generated in different zones of the container. Under appropriate circumstances, the vortices may lead to mixing. The flow details are obtained by numerical integration of time dependent governing equations for mass, momentum and energy. The flow visualization is obtained using Lagrangian particle tracking of a set of points distributed on a closed surface. The deformation of the surface contains information about dynamics of the flow; in particular, it is possible to identify zones where flow stretching and foldings occur. An estimation of the error by reversal is given. Calculations and visualizations were made in an Origin 2000 and in an Onix computer respectively.
Computational Fluid Dynamics (CFD) is concerned with modeling fluid flows by means of numerical solutions of the conservation equations. In the present days, increasingly sophisticated software and hardware is being developed to simulate interesting flow phenomena. In general, CFD simulations provide large sets of numbers that describe the velocity, pressure, density etc. fields produced by solving the governing equations for mass, momentum and energy. In order to translate the information contained in the sets of numbers into a more readily understandable form, several visualization techniques have been developed. In fact, for complicated, time-dependent, three dimensional flows, visualization has become an indispensable tool for understanding the qualitative features of flows.
In steady flows, a streamline is a line tangent to the velocity field at an instant in time. For unsteady flows, three types of particle traces have been defined: pathlines, streaklines and timelines. A pathline shows the trajectory of a single particle released from one fixed position, called seed location, and followed as the velocity field change in time. A streakline is a line joining the positions, at an instant in time, of all particles that have been previously released from a seed location. A timeline is a line connecting particles that have been released from different positions at the same time. See [1].
We work with natural convective mixing flows and due to the complex three-dimensional topology of the flow, unidimensional and bidimensional sections of fields do not reflect clearly some of its properties. For this reason, it has been necessary to devise new techniques to visualize interesting flow characteristics.
In this work, we extend the particle tracking technique to Lagrangian surface tracking. Using surface tracking, it is possible understand different aspects of the flow, especially in mixing flows.
Surface tracking consist in defining a set of points arbitrarily distributed on a surface. Then we follow the motion of these fluid parcels, as a pathlines, and get a deformed surface that contains information about the dynamics of the problem.
All calculations required for the examples presented were obtained using an Origin 2000. The graphics were obtained using the software Alias Power/Animator that produce spectacular and, in some sense, realistic images. These graphics were performed in an Onix Reality Engine.
We consider a cubic prism filled with a Newtonian fluid and with Prandtl number equal to 200. The gravity is pointing in the negative vertical direction. The left and right walls of the prism are kept at a constant temperature in all area but oscillating in time following the functions defined in equations 9 and 10. The rest of the walls are considered adibatic. The governing equations in terms of nondimensional variables are:
The Rayleigh (Ra) and Prandtl (Pr) numbers are defined by
y
Where g is the acceleration due to gravity and 
is volumetric thermal expansion coefficient. u,v, and w are velocity components: 
. P and T are the temperature and pressure respectively
The boundary conditions required for the solution are:
The individual cycles of functions 
and 
are defined by
is the rate of change of temperature for the walls and 
are the relative phases of heating and cooling for left and right walls. The following initial conditions are assumed:
The numerical results were obtained using a suitably modified version of 3Dbox program [2] that solves the time-dependent, three-dimensional, governing equations in primitive variables. The code is based on
In this work, we used a discretization mesh of 
volumes and nondimensional time step was 
.
Particle tracking is based on a numerical integration of an ordinary differential equation (ODE). Given a vector function 
defined for all 
in the grid domain G at an instant of time t, the path of a massless particle at position can be determined by solving the following ODE:
The function 
represent the position of the particle at time t, and is the velocity field. The starting position 
of the particle provides the initial condition:
The solution is a sequence of particle positions 
.
A particle tracking algorithm must perform the following steps. First a search is performed for the cell which contains the initial position of the particle. Once the container cell is found, we have to determine the velocity at the initial position, therefore the velocities at the cell corners must be interpolated. Then, an integration step calculates the next position. The process of interpolation, integration and point location is repeated until the particle leaves the grid. The pseudocode of this process is as follows:
find cell containing initial position
while particle in grid
determine velocity at current position
calculate new position
find cell containing new position
endwhile
The above code shows only the main algorithm components; in real implementations many refinements and optimizations are required.
The first step in the particle tracking algorithm is determining which cell contains a specified point. The coordinates of a point can be divided into their integer and fractional parts: 
, where i,j,k are integers and 
. In many texts [i,j,k] are referred to as indices and 
as offsets. Point location is as simple as truncating the coordinates to their integer parts. The integer parts give the cell where the point is located. Here, determining the offsets is also considered to be part of the point location operation, but sometimes we will strictly distinguish between point location and offset determination. The offsets are used to make a weighted interpolation.
The velocity at the current position of the particle is required to advance the particle. In order to obtain a value of the velocity field at points other than the grid nodes, it is necessary to determine an interpolated value using the velocities at the corners of the grid cell that contains the point. The standard way to do this in cubical cells is trilinear interpolation. This scheme is fast and simple. If is in grid cell [i,j,k] and has the fractional offsets , then
where 
is the velocity at grid point (i,j,k). The trilinear interpolation assumes that the velocity varies linearly across the edges of the cell. Though trilinear interpolation is simple, accuracy may be lost if the grid is coarse or deformed. Yeung and Pope [6] compared higher-order interpolations to linear interpolation.
The integration methods used were a first-order Euler scheme and the fourth-order Runge-Kutta. The positions of the particle as the time is incremented can be computed integrating equation 11. Hence, the particle position after time 
is as follows:
If we consider that the velocity is constant in the interval 
, then the solution to the above equation is
This is the most simple integration method and is known as the Euler formula. The right side contains the two first terms of a Taylor series. A more accurate integration scheme is the Runge-Kutta method of fourth-order. This method consist in the next steps:
Let 
, k = 0 and 
be the current position of the particle. Then for 
and on G, let
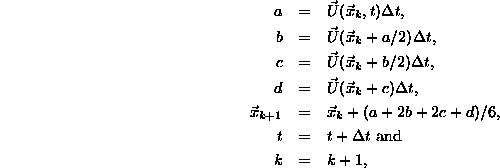
This process is repeated until 
.
In this work we use both Euler and fourth-order Runge-Kutta methods to make particle tracking.
The result of solving the equations of balance is a set of pressure, temperature and velocity fields as time and position function. The velocity field is defined on each node of the mesh used for numerical integration. The Eulerian velocity gives little information about certain aspects of flow dynamics, in particular details of mixing and the typical ways of visualizing a flow (streamlines, pathlines, and to a lesser degree, streaklines) are insufficient to completely understand the process. Our problem begins rather than ends with specification of . The solution of 11 with 
at time 
, provides the starting point for our analysis.
Lagrangian tracking of surfaces is the direct generalization of particle tracking. The process is as follows:
First, we define an initial surface, at initial time t, inside of the fluid container. This surface is defined as a set of points 
localized in convenient positions, but at first arbitrary. After a time , the surface is formed with a set of points 
. This set of points are calculated using the particle tracking algorithm described in Section 3. We applied the algorithm to each point on the surface. The result is a deformed surface following the velocity field. The deformation of the surface will give then information about the flow's general dynamics and in particular it will allow to know zones where neighboring points will separate by the stretchings, or zones of volume where the surface is folding, permiting that points originaly far away come together.
The algorithm for particle tracing was coded in Fortran 77 and executed on an Origin 2000 with 32 processors. For surface tracking it is easy make a parallelization using some directives for the compiler. Because the points on the surface are independent each other, it is possible to calculate the trajectory of each point concurrently.
The code is as follows:
C$DOACROSS
do i=1,N
CC Point Location ...
CC Interpolation ...
CC Integration ...
enddo
The above loop is executed for each point on the surface, then N is the total number of points that defines the surface.
The directive C$DOACROSS automatically parallalize the loop if the compilation is doing with the argument -mp.
We present three examples that highlight the avantages of the flow visualization described in the previous subsection.
In an effort to obtain an estimation of the error in the visualization method, a calculation was made starting with a deformed surface and reversing the sign of the velocity vector field. In principle, the deformed surface should return to the shape of a sphere. Figure 11 shows the result of this process using fourth-order Runge-Kutta integration. This image can be compared with figure 12 where the same process is shown using an Euler integration. The largests departure from the spherical surface is in the lower hemisphere in the region near the mid z-plane. A graphic of an intersection with the mid z-plane is shown in figure 13, where Runge-Kutta and Euler formulations are compared with the initial circle.
The mixing effect is evident thanks to visualization of deformed surfaces by Lagrangian tracking. The combined techniques of numerical solution of equations and realistic visualization of results, make it possible have a better understanding of flow dynamics. In particular was possible to indentify stretching and folding zones in the flow. Moreover, using time reversal and surface tracking, was possible to find zones of the flow where the numerical error has a maximum. In future, we will attempt to improve the spatial resolution of discretization and to increase the number of points that define the surfaces of analysis. Also is essential to device a theory that allows to do an exact analysis of errors involved in the calculations.
This study was supported by UNAM-Cray Fund and CONACyT project G0044-E. This work was based on some codes for graphics building developed by Wendy Aguilar Martinez her help is gratefully acknowledged.
Figure 3: Surface tracking. An sphere with a mesh at initial time.
Figure 4: Deformed surface at 320 non-dimensional time units.
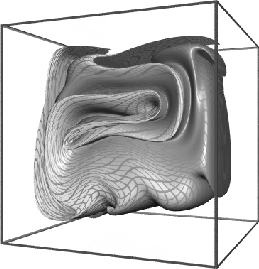
Figure 5: Deformed surface at 640 non-dimensional time units.
Figure 6: Two little spheres at initial time.
Figure 7: Deformed spheres after 20 cycles (1600 non-dimensional time units).
Figure 8: Two small spheres at initial time. One sphere is out of the mid z-plane.
Figure 9: Deformed spheres after 20 cycles (1600 non-dimensional time units).
Figure 10: View of figure 9 from x-axis.
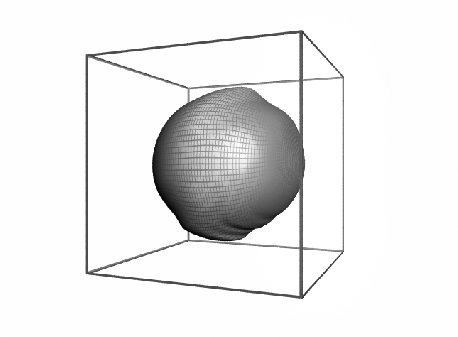
Figure 11: Time reversal using fourth-order Runge-Kutta formula.
Figure 12: Time reversal using Euler formula. The error is greater than that shown in figure 11.
