B. Ujfalussy, Xindong Wang, Xiaoguang Zhang, D. M. C. Nicholson,
W. A. Shelton, and G. M. Stocks,
Oak Ridge National Laboratory, Oak Ridge, TN 37831,
- A. Canning,
NERSC, Lawrence Berkeley National Laboratory, Berkeley, CA 94720,
- Yang Wang,
Pittsburgh Supercomputing Center, Pittsburgh, PA 15213,
- B. L. Gyorffy,
H. H. Wills Physics Laboratory, University of Bristol, Bristol, UK.
The understanding of metallic magnetism is of fundamental importance for a wide range of technological applications ranging from thin film disc drive read heads to bulk magnets used in motors and power generation. We use the power of massively parallel processing (MPP) computers to perform first principles calculations of large system models of non-equilibrium magnetic states in metallic magnets. The constrained LSMS method we have developed exploits the locality in the physics of the problem to produce an algorithm that has only local and limited communications on parallel computers leading to very good scale-up to large processor counts and linear scaling of the number of operations with the number of atoms in the system. The computationally intensive step of inversion of a dense complex matrix is largely reduced to matrix-matrix multiplies which are implemented in BLAS. Throughout the code attention is paid to minimizing both the total operation count and total execution time, with primacy given to the latter. Full 64-bit arithmetic is used throughout. The code shows near linear scale-up to 1458-processing elements (PE) and attained a performance of 1.02 Tflops on a Cray T3E1200 LC1500 computer at Cray Research. Additional performance figures of 657 and 276 Gflops have also been obtained on a Cray T3E1200 LC1024 at a US Government site, and on a T3E900 machine at the National Energy Research Scientific Computing Center (NERSC) respectively. All performance figures include necessary I/O.
We used the power of massively parallel processing (MPP) computers to implement a new first principles constrained local moment (CLM) theory of non-equilibrium states in metallic magnets that has allowed us to perform the first calculations of CLM states for Iron above its Curie temperature ( ![]() ), where the bulk magnetization vanishes even though individual atomic moments remain. This CLM state can be thought of as being prototypical of the magnetic order at a particular step in a Spin Dynamics (SD) simulation of the time and temperature dependent properties of metallic magnets. In the specific calculations that we have performed magnetic moments associated with individual Fe atoms in the solid are constrained to point in a set of orientations that is chosen using a random number generator. The infinite solid is modeled using large unit cells containing up to 1458 Fe atoms with periodic boundary conditions.
), where the bulk magnetization vanishes even though individual atomic moments remain. This CLM state can be thought of as being prototypical of the magnetic order at a particular step in a Spin Dynamics (SD) simulation of the time and temperature dependent properties of metallic magnets. In the specific calculations that we have performed magnetic moments associated with individual Fe atoms in the solid are constrained to point in a set of orientations that is chosen using a random number generator. The infinite solid is modeled using large unit cells containing up to 1458 Fe atoms with periodic boundary conditions.
The electronic/magnetic structure problem is solved using constrained density functional theory in the local spin density approximation (constrained LSDA). A feature of the new theory is the introduction of self-consistently determined site dependent magnetic fields that serve to constrain the local magnetic moments to a prescribed set of directions. The formidable task of solving the self-consistent field (SCF) equations of constrained LSDA for large unit cell models is accomplished using the locally self-consistent multiple scattering method (LSMS) extended to treat non-collinear magnetism and to include the constraining fields. The basic LSMS method is an O(N) LDA method that was specifically designed for implementation on MPPs and for treating the quantum mechanical interactions between large numbers of atoms.
Using the constrained non-collinear LSMS code we have performed calculations of CLM states in paramagnetic Fe using Cray T3E MPPs at the National Energy Research Supercomputer Center (NERSC), at Cray, Eagan (a Division of Silicon Graphics), at NASA Goddard Space Flight Center, and at a US Government (USG) site. The major achievements reported in this paper are:
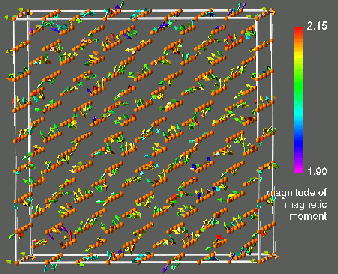
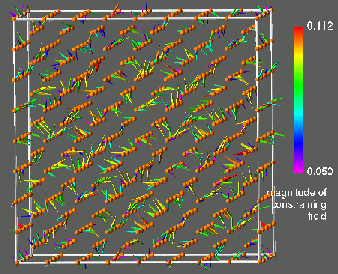
Figure 1: Visualization of results obtained for a 512-atom CLM state of prototypical paramagnetic bcc Fe. The left frame shows the magnetic moments, the right frame shows the corresponding transverse constraining fields. Atom positions are denoted by spheres, magnetic moments by arrows and constraining fields by cones. There magnitudes are color coded as indicated. These calculations are for LIZ27 and were performed on the T3E900 LC512 at NERSC.
The local density approximation (LDA) to density functional theory (DFT, [3]) is now the accepted way of performing first principles electronic structure and total energy calculations for condensed matter. Density functional theory is an exact theory of the ground state. The LDA converts DFT into a practical computational scheme. DFT-LDA replaces the solution of the many particle Schrödinger equation by the solution of a set of single particle self-consistent field (SCF) equations. The complex many body exchange and correlation effects are included through an effective exchange correlation potential. In DFT the central quantities of interest are the charge density ![]() (and in LS(pin)DA the magnetization density
(and in LS(pin)DA the magnetization density ![]() ). For a fixed external potential (e.g. that resulting from a set of nuclei) DFT-LDA returns the ground state
). For a fixed external potential (e.g. that resulting from a set of nuclei) DFT-LDA returns the ground state ![]() (and
(and ![]() ). For non-spin-polarized systems the SCF equations take the form:
). For non-spin-polarized systems the SCF equations take the form:
The SCF algorithm proceeds as follows: an input guess ![]() of the electronic charge is used in eq. 3 to construct an initial guess of the effective electron-ion potential
of the electronic charge is used in eq. 3 to construct an initial guess of the effective electron-ion potential ![]() appearing in the Schrödinger equation (eq. 1). The single particle Schrödinger equation is solved to obtain the single particle wave functions or, as indicated in eq. 1 and as is appropriate to the multiple scattering Greens function methods used in this paper, the single particle Greens function,
appearing in the Schrödinger equation (eq. 1). The single particle Schrödinger equation is solved to obtain the single particle wave functions or, as indicated in eq. 1 and as is appropriate to the multiple scattering Greens function methods used in this paper, the single particle Greens function, ![]() , from which an output charge density
, from which an output charge density ![]() can be obtained using eq. 2. A new
can be obtained using eq. 2. A new ![]() is constructed by mixing the original
is constructed by mixing the original ![]() with
with ![]() according to some (linear or non-linear) mixing algorithm. This procedure is then iterated until
according to some (linear or non-linear) mixing algorithm. This procedure is then iterated until ![]() and
and ![]() agree to prescribed small tolerance. Once a SCF solution is found the total energy is obtained from:
agree to prescribed small tolerance. Once a SCF solution is found the total energy is obtained from:
Cleary, LDA is a first principles, parameter free, theory of matter in that the only inputs are the atomic numbers of the constituent elements.
Standard ![]() -space electronic structure methods for solving the LDA single particle Schrödinger equation (eq. 1) ultimately scale as the third power of the number of atoms, N, in the unit cell. This is due to the need to diagonalize, invert, or orthogonalize a matrix whose size is proportional to N. For the very large cells that are required for implementing SD this scaling is prohibitive. The LSMS method [2] avoids this
-space electronic structure methods for solving the LDA single particle Schrödinger equation (eq. 1) ultimately scale as the third power of the number of atoms, N, in the unit cell. This is due to the need to diagonalize, invert, or orthogonalize a matrix whose size is proportional to N. For the very large cells that are required for implementing SD this scaling is prohibitive. The LSMS method [2] avoids this ![]() scaling by using real space multiple scattering theory to obtain the Green function (eq. 1) and hence the electronic charge (eq. 2) and magnetization densities. In the LSMS method the atoms comprising the crystal are treated as disjoint electron scatterers. The multiple scattering equations are solved for each atom by ignoring multiple scattering processes outside a local interaction zone (LIZ) centered on each atom (see figure 2).
scaling by using real space multiple scattering theory to obtain the Green function (eq. 1) and hence the electronic charge (eq. 2) and magnetization densities. In the LSMS method the atoms comprising the crystal are treated as disjoint electron scatterers. The multiple scattering equations are solved for each atom by ignoring multiple scattering processes outside a local interaction zone (LIZ) centered on each atom (see figure 2).
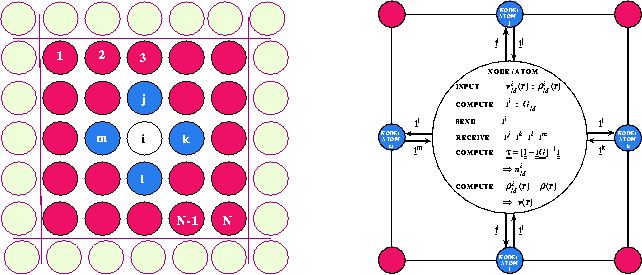
Figure 2: Left Schematic of a parallel SCF algorithm. We envision a basic unit cell consisting of N-atoms labeled ![]() which is periodically reproduced as indicated. About each atom, for example the
which is periodically reproduced as indicated. About each atom, for example the ![]() , we define a local interaction zone consisting of M-atoms including itself, for example labeled i,j,k,l,m. Right Schematic of the implementation LSMS algorithm on a massively parallel computer.
, we define a local interaction zone consisting of M-atoms including itself, for example labeled i,j,k,l,m. Right Schematic of the implementation LSMS algorithm on a massively parallel computer.
The potential throughout the whole space is reconstructed in the standard way by solving Poisson's equation (eq. 3) for a crystal electron density made up of a sum of the single site densities. Clearly, the LIZ size is the central convergence control parameter for the method. For face and body centered cubic (fcc and bcc) transition metals LIZ sizes of a few ( ![]() ) neighboring atom shells are sufficient to obtain convergence of the charge and magnetization densities. Using an Intel Paragon XP/S-150, quite precise O(N) scaling of the basic LSMS method has been demonstrated previously for up to 1024 atom(nodes) [2].
) neighboring atom shells are sufficient to obtain convergence of the charge and magnetization densities. Using an Intel Paragon XP/S-150, quite precise O(N) scaling of the basic LSMS method has been demonstrated previously for up to 1024 atom(nodes) [2].
The details of the LSMS method have been described in the literature [2]. The extension to cover the case of non-collinear moment arrangements is discussed in appendix A. Here let us simply quote the two most salient formulae necessary to understand the basic algorithm. The first is the Green's function for the atom at the center of the LIZ, ![]() , which is given by
, which is given by
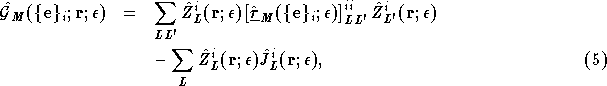
The second is the scattering path matrix, ![]() , which describes the multiple scattering effects within the LIZ. It is given by the inverse of the KKR matrix,
, which describes the multiple scattering effects within the LIZ. It is given by the inverse of the KKR matrix, ![]() , through
, through
In the last equation ![]() is the t-matrix which describes the scattering from a single site and
is the t-matrix which describes the scattering from a single site and ![]() is the structure constant matrix which describes the propagation of electrons from site to site. The above matrices are matrices in site (i), angular momentum (L) and spin (denoted by
is the structure constant matrix which describes the propagation of electrons from site to site. The above matrices are matrices in site (i), angular momentum (L) and spin (denoted by ![]() ) indices. This gives a linear dimension of
) indices. This gives a linear dimension of ![]() , where M is the number of atoms in the LIZ (in our runs 13, 27 or 65), L is a combined angular and azimuthal quantum number (16 for atoms near the center of the LIZ and 9 for the more distant ones), and the factor of 2 arises from the spin index. In this work the largest matrix size that we encountered was 1548. Not surprisingly, inversion of the KKR matrix (eq. 6) to obtain the scattering path matrix is the most time consuming task in the LSMS method.
, where M is the number of atoms in the LIZ (in our runs 13, 27 or 65), L is a combined angular and azimuthal quantum number (16 for atoms near the center of the LIZ and 9 for the more distant ones), and the factor of 2 arises from the spin index. In this work the largest matrix size that we encountered was 1548. Not surprisingly, inversion of the KKR matrix (eq. 6) to obtain the scattering path matrix is the most time consuming task in the LSMS method.
A general orientational configuration of atomic magnetic moments ![]() like the one in figure 1 (left) is not a ground state of LSDA. In order to properly describe the energetics of a general configuration it is necessary to introduce a constraint which maintains the orientational configuration. The purpose of the constraining fields is to force the local magnetization,
like the one in figure 1 (left) is not a ground state of LSDA. In order to properly describe the energetics of a general configuration it is necessary to introduce a constraint which maintains the orientational configuration. The purpose of the constraining fields is to force the local magnetization, ![]() , to point along the prescribed local direction
, to point along the prescribed local direction ![]() . Figure 1 (right) shows the constraining fields corresponding to the magnetic moments obtained in our 512-atom simulation of the CLM state in paramagnetic Fe (fig. 1 (left)). Note that at each site the constraining field is transverse to the magnetization. The constraining field is not known a priori, and has to be calculated by some additional algorithm. The details of the theory and the constrained local moment model are contained in reference [1].
. Figure 1 (right) shows the constraining fields corresponding to the magnetic moments obtained in our 512-atom simulation of the CLM state in paramagnetic Fe (fig. 1 (left)). Note that at each site the constraining field is transverse to the magnetization. The constraining field is not known a priori, and has to be calculated by some additional algorithm. The details of the theory and the constrained local moment model are contained in reference [1].
By making an atom (or atoms) to node equivalence the LSMS is highly scalable on MPPs since each node can be assigned the work involved in setting up and inverting the KKR matrix eq. (6) for the atom(s) to which it is assigned. Inversion of the KKR matrix is the most time consuming step in the LSMS method. As can be seen in figure 3, it dominates the calculation via it's implementation in terms of complex matrix-matrix multiplies using the highly optimized BLAS routine CGEMM.
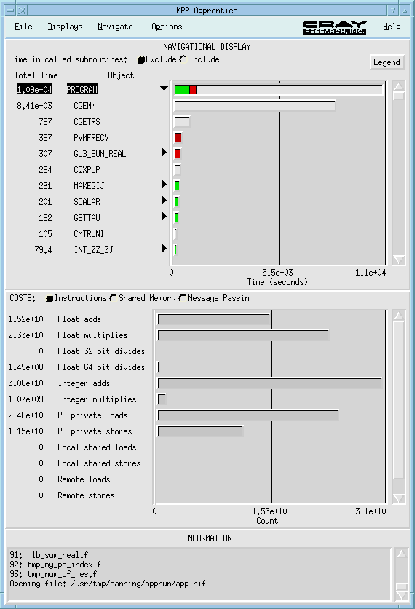
Figure 3: Screen dump from an apprentice performance run for a 16 atom system for 5 SCF iterations. The apprentice performance tool does not give flop counts for routines such as CGEMM that are coded in assembler so the flop counts in the lower half of the window are incorrect (see text for more details). This figure is included to show the percentage of time the code takes in each of the most important subroutines. CGEMM is a BLAS complex matrix-matrix multiply and CGETRS is an LAPACK routine for solving systems of linear equations. PVMFRECV is the PVM message receiving routine and the time for this routine plus the time for GLB_SUM_REAL is very close to the total time spent in communications as the other PVM routines take a negligible amount of time.
Keeping angular momenta up to ![]() the dimension of the matrix that is inverted is
the dimension of the matrix that is inverted is ![]() , where M is the number of atoms in the LIZ and the factor of 2 comes from the spin-index. Calculation of the charge and magnetization densities (eqs. 15 and 16) requires that each node invert a matrix of dimension
, where M is the number of atoms in the LIZ and the factor of 2 comes from the spin-index. Calculation of the charge and magnetization densities (eqs. 15 and 16) requires that each node invert a matrix of dimension ![]() for a set of energies along a contour in the complex energy plane of sufficient density to converge the energy integrals in eqs. 15 and 16. If M is smaller than the number of atoms in the system, N, this is clearly advantageous compared to conventional reciprocal space methods since these involve the inversion of a matrix of dimension
for a set of energies along a contour in the complex energy plane of sufficient density to converge the energy integrals in eqs. 15 and 16. If M is smaller than the number of atoms in the system, N, this is clearly advantageous compared to conventional reciprocal space methods since these involve the inversion of a matrix of dimension ![]() at a sufficient number of
at a sufficient number of ![]() points to converge necessary Brillouin zone integrals. The details of how the LSMS algorithm maps onto a parallel machine is shown in figure 2 (left) and explained in detail in the literature[2].
points to converge necessary Brillouin zone integrals. The details of how the LSMS algorithm maps onto a parallel machine is shown in figure 2 (left) and explained in detail in the literature[2].
Necessary message passing involves passing of single site t-matrices for the sites/nodes in a given atoms LIZ, as well as global information regarding the total charge in the system, charge transfer and potential multipole moments. As can be seen from the "Apprentice" screen dump shown in figure 3, message-passing is limited (it is also mainly local). This is a direct result of the complete rethinking of the electronic structure problem in terms of a parallel algorithm. This allows the algorithm to scale up to very large numbers of processors with the percentage of time spent in communications staying approximately constant when the number of processors increases with the number of atoms.
In the LSMS method each node calculates the scattering path matrix for it own atom(s). Hence, only the ![]() (
( ![]() ) upper left block of the inverse is required, which represents the local atom's contribution to the scattering path matrix. A significant enhancement in computational performance can be achieved by taking advantage of this fact. Furthermore, the design of the inversion algorithms can be largely based on BLAS level 3 matrix-matrix multiply routines to ensure optimal performance.
) upper left block of the inverse is required, which represents the local atom's contribution to the scattering path matrix. A significant enhancement in computational performance can be achieved by taking advantage of this fact. Furthermore, the design of the inversion algorithms can be largely based on BLAS level 3 matrix-matrix multiply routines to ensure optimal performance.
Two approaches were followed, one was to use direct methods and the other was to investigate non-symmetric iterative methods. The idea of using iterative methods stems from the fact that the upper ![]() block of the inverse can be efficiently solved for as a system of linear equation with only L right hand sides. The implementation of the iterative method was enhanced by using a block iterative approach where the matrix-vector multiply is replaced by a matrix-matrix multiply and all the right-hand sides are iterated simultaneously. The final algorithm was a hybrid algorithm that switches between a direct method developed by one of us (XGZ) [5] that is based on a variant of Strassen's method [6, 7, 8] and a true fixed storage minimal-residual iterative method (MAR1) developed by Kosmal and Nissel [12]. All of these algorithms are substantially faster than straightforward use of the LAPACK LU routines.
block of the inverse can be efficiently solved for as a system of linear equation with only L right hand sides. The implementation of the iterative method was enhanced by using a block iterative approach where the matrix-vector multiply is replaced by a matrix-matrix multiply and all the right-hand sides are iterated simultaneously. The final algorithm was a hybrid algorithm that switches between a direct method developed by one of us (XGZ) [5] that is based on a variant of Strassen's method [6, 7, 8] and a true fixed storage minimal-residual iterative method (MAR1) developed by Kosmal and Nissel [12]. All of these algorithms are substantially faster than straightforward use of the LAPACK LU routines.
Although both direct and iterative methods are present in the code, in the performance runs discussed later, we used the blocked direct method, which turned out to be the most efficient for this application.
The runs were performed on Cray T3E machines at the National Energy Research Scientific Computing Center (NERSC) at the Lawrence Berkeley National Laboratory (LBNL), Berkeley (T3E900 LC512); Cray, Eagan (T3E1200 LC1500 and T3E1200 LC512); NASA Goddard Space Flight Center (T3E600 LC1024) and a T3E1200 LC1024 at a US Government site. The T3E900 at NERSC has 544 EV5, 450 MHz, DEC processors, 512 of which are available for applications and the remaining 32 are used as command, OS and spare processors. The EV5 can perform two floating point operations per cycle so this gives the processor a peak speed of 900 Mflops and the machine a peak speed of 460 Gflops. Each processor has 256 MB of memory and there is an additional 1.4 TB of disk storage. The T3E600 and T3E1200 have 300 Mhz and 600 Mhz processors giving the LC1024 machines peak speeds of 614 Gflops and 1.22 Tflops respectively.
The code was compiled using version 3.0.2.1 of the Cray cf90 and cc compilers; version 3.0.2.0 of Craylibs which contains the Cray version of the BLAS routines and other scientific libraries and version 1.2.0.2 of mpt which contains the PVM libraries. The code was compiled with compiler options (f90 -c -dp) for Fortran90 routines and (cc -c -O2) for the C routines. Since the code spends a large percentage of its time in library routine calls there is essentially no speedup using optimization flags in the compilation. The code was run under version 2.0.3.10 of the Unicosmk operating system.
The CLM version of the LSMS code is written in FORTRAN and is approximately 40,000 lines. The compiled T3E node executable is 0.363 MW. The data for each atom occupies approximately 6 MW of memory for the large runs. Message passing is implemented in both PVM and NX, the native message passing of the Intel Paragon. A pre-processor is used to select the particular environment for which the code is being compiled. The code will run in a single atom mode on a workstation, and in multi-atom mode on collections of workstations, the Intel Paragon and Cray T3E. For systems having some symmetry a single node can represent all symmetry related atoms in the system. The code is written in such a way that, on machines which support multiple PVM processes per processor, one PE may handle multiple atoms.
The crystalline phase of iron is body centered cubic (bcc) with a lattice constant of 5.27 a.u. Calculations were performed on systems constructed from orthorhombic cells that are ![]() repeats of the underlying bcc primitive cell to yield cells containing 2, 8, 16, 54, 128, 256, 512, 1024 and 1458 iron atoms. All calculations are performed using periodic boundary conditions. The orientational configuration of magnetic moments was obtained from a random number generator. The constraining fields were initialized to zero. The charge density, magnetic moments and constraining fields were iterated to convergence (selfconsistency). We found that the constraining fields converged rapidly (a few tens of iterations), while convergence of the charge and magnetization densities required
repeats of the underlying bcc primitive cell to yield cells containing 2, 8, 16, 54, 128, 256, 512, 1024 and 1458 iron atoms. All calculations are performed using periodic boundary conditions. The orientational configuration of magnetic moments was obtained from a random number generator. The constraining fields were initialized to zero. The charge density, magnetic moments and constraining fields were iterated to convergence (selfconsistency). We found that the constraining fields converged rapidly (a few tens of iterations), while convergence of the charge and magnetization densities required ![]() 800 iterations.
800 iterations.
To speed up convergence we initially performed calculations with an LIZ of one nearest neighbor shell. This gives a matrix of size of ![]() for the matrix inversion on each processor. In this case, one SCF iteration took 14.13 seconds (averaged over 50 SCF iterations). Once we were able to obtain reasonably selfconsistent potentials, the size of the LIZ was increased to three nearest neighbor shells and the convergence continued. This gives a matrix size of
for the matrix inversion on each processor. In this case, one SCF iteration took 14.13 seconds (averaged over 50 SCF iterations). Once we were able to obtain reasonably selfconsistent potentials, the size of the LIZ was increased to three nearest neighbor shells and the convergence continued. This gives a matrix size of ![]() for which one SCF iteration takes an average of 132.11 seconds (average taken over a 10 SCF iteration run). Finally, to obtain well converged moments and constraining fields the LIZ was increased to six nearest neighbor shells. This gives a matrix size of
for which one SCF iteration takes an average of 132.11 seconds (average taken over a 10 SCF iteration run). Finally, to obtain well converged moments and constraining fields the LIZ was increased to six nearest neighbor shells. This gives a matrix size of ![]() for which one SCF takes 499.91 seconds (averaged over 5 iterations). In the following we quote performance figures for two types of runs corresponding to three nearest neighbor shells (denoted by LIZ27) and six nearest neighbor shells (denoted by LIZ65).
for which one SCF takes 499.91 seconds (averaged over 5 iterations). In the following we quote performance figures for two types of runs corresponding to three nearest neighbor shells (denoted by LIZ27) and six nearest neighbor shells (denoted by LIZ65).
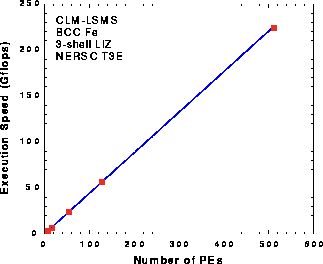
Figure 4: Illustration of the speedup for 8, 16, 54, 128 and 512 nodes/atoms. The ideal (linear) speedup is indicated by the continuous line, measured values for the LIZ27 runs are shown as squares.
In figure 4 we illustrate the scaling of the LSMS algorithm with the number of atoms/nodes in the system for LIZ27 runs. The solid line shows ideal linear speedup, extrapolated from the 8 node run. The solid squares are the measured speeds observed for runs with 8, 16, 54, 128 and 512 nodes. Scale up from 512 to 1024 atoms during LIZ65 runs showed continued excellent scaling.
The Cray Apprentice performance tool on the T3E is a software performance tool and does not provide flop counts for assembly coded routines such as CGEMM. In order to obtain the flop count of the LSMS code we ran it on a Cray J90 using the hardware performance monitor. This code uses no parallel libraries so the code and flop count on the J90 and T3E are the same. For each atom the total numbers of floating point operations (flop) for one SCF iteration were ![]() and
and ![]() floating point operations for the LIZ27 and LIZ65 runs respectively (see appendix B for details of the J90 hardware performance monitor runs). Due to the nature of the method the total number of operations scales linearly with the number of atoms. Consequently, it is straightforward to calculate the total performance on the T3E (
floating point operations for the LIZ27 and LIZ65 runs respectively (see appendix B for details of the J90 hardware performance monitor runs). Due to the nature of the method the total number of operations scales linearly with the number of atoms. Consequently, it is straightforward to calculate the total performance on the T3E ( ![]() ) for the systems we ran using the formula:
) for the systems we ran using the formula:
![]()
where ![]() is the number of nodes (atoms),
is the number of nodes (atoms), ![]() is the run time per SCF iteration and
is the run time per SCF iteration and ![]() is the appropriate floating point operation count. The largest simulation performed was of 1458 atoms on 1458 processors of a T3E1200 LC1500 at Cray Research, Eagan,for which we obtained a performance of 1.02 Tflops for a five SCF iteration LIZ113 run. A simulation of 1024 atoms on a 1024 processor USG site T3E1200 LC1024 ran at 657 Gflops for a five SCF iteration LIZ65 run. This run won the Gordon Bell Prize at last years SC98. Performance figures for LIZ65 512 atom calculations on 512 processors on the NERSC T3E900 LC512 and a Cray Research T3E1200 LC512 were 276 and 329 Gflops respectively. The corresponding LIZ27 performances are 224 and 264 Gflops. For LIZ65 runs on the 600 MHz machines the single node performance is 641.06 Mflops which is a substantial fraction of the 762 Mflops CGEMM benchmark performance for a
is the appropriate floating point operation count. The largest simulation performed was of 1458 atoms on 1458 processors of a T3E1200 LC1500 at Cray Research, Eagan,for which we obtained a performance of 1.02 Tflops for a five SCF iteration LIZ113 run. A simulation of 1024 atoms on a 1024 processor USG site T3E1200 LC1024 ran at 657 Gflops for a five SCF iteration LIZ65 run. This run won the Gordon Bell Prize at last years SC98. Performance figures for LIZ65 512 atom calculations on 512 processors on the NERSC T3E900 LC512 and a Cray Research T3E1200 LC512 were 276 and 329 Gflops respectively. The corresponding LIZ27 performances are 224 and 264 Gflops. For LIZ65 runs on the 600 MHz machines the single node performance is 641.06 Mflops which is a substantial fraction of the 762 Mflops CGEMM benchmark performance for a ![]() complex matrix-matrix multiply. LIZ27 runs on the NASA Goddard Space Flight Center (T3E600 LC1024) yielded a performance of 343 Gflops. It should be noted that all these performance figures include all message passing and I/O time.
complex matrix-matrix multiply. LIZ27 runs on the NASA Goddard Space Flight Center (T3E600 LC1024) yielded a performance of 343 Gflops. It should be noted that all these performance figures include all message passing and I/O time.
We wish to thank the Cray staff and in particular Steve Caruso, Mike Stewart and Steve Luzmoor at NERSC, Martha Dumler and William White at Cray, Eagan, and Tom Clune at NASA, Goddard, for their help and also the NERSC staff in particular Mike Welcome of the systems group. We are also grateful NASA Goddard Space Flight Center for allowing us access to their machine which allowed us several 1024-node crucial debugging runs as well as final performance runs. Work supported by Office of Basic Energy Sciences, Division of Materials Sciences, and Office of Computational and Technology Research, Mathematical Information and Computational Sciences Division, US Department of Energy, under subcontract DEAC05-960R22464 with Lockheed-Martin Energy Research Corporation and DEAC03-76SF00098. Access to the Cray T3E-600 was provided by the Earth and Space Sciences (ESS) component of the NASA High Performance Computing and Communications (HPCC) Program. One of us (BU) is supported by an appointment to the Oak Ridge National Laboratory Postdoctoral Research Associates Program administered jointly by the Oak Ridge National Laboratory and the Oak Ridge Institute for Science and Education. This work was carried out as part of the Department of Energy materials science grand challenge project which is a joint project between Oak Ridge National Laboratory, Ames Laboratory (Iowa), Brookhaven National Laboratory, the National Energy Research Scientific Computing Center at Lawrence Berkeley Laboratory, and the Center for Computational Science at the Oak Ridge National Laboratory.
Appendices
For non-collinear spin systems, it is necessary to re-formulate the multiple scattering approach so that its applications are not limited to the case where spins are parallel or antiparallel to the z-axis. Here we give a quick summary of this generalization. The Schrödinger equation for the crystal becomes
![]()
where ![]() is a sum of single site one-electron potentials,
is a sum of single site one-electron potentials, ![]() , and
, and
![]()
where ![]() is a sum of single site one-electron potentials,
is a sum of single site one-electron potentials, ![]() , and
, and
![]()
Assuming that on site i, the local potential ![]() can be diagonalized by a unitary transformation
can be diagonalized by a unitary transformation ![]() , i.e.,
, i.e.,
![]()
we call this diagonal form of single site potential the local frame. It is easy to show that
where ![]() is the vector of Pauli spin matrices.
is the vector of Pauli spin matrices.
In the LSMS for non-collinear magnetism, the Green's function in spin space is a ![]() matrix and, in the vicinity of site i, is given by
matrix and, in the vicinity of site i, is given by
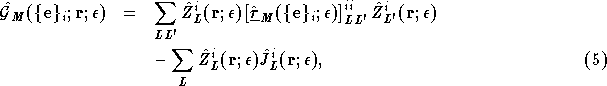
where M is the number of atoms in the LIZ of atom i, ![]() represents a magnetic configuration of the atom cluster in the LIZ, and
represents a magnetic configuration of the atom cluster in the LIZ, and ![]() is the scattering path matrix for the cluster of atoms in the LIZ, obtained from the matrix inversion
is the scattering path matrix for the cluster of atoms in the LIZ, obtained from the matrix inversion
Here the matrices have site, angular momentum and spin indices.
If we restrict ourselves to muffin tin potentials, the electron density and the magnetization density on the central site is given by a straightforward generalization of the formulae given by Faulkner and Stocks [4]:
and
where ![]() is the Fermi-Dirac function,
is the Fermi-Dirac function, ![]() is the chemical potential of the system.
is the chemical potential of the system.
The following are outputs from the hardware performance monitor (HPM) on the NERSC Cray J90 computer "killeen". We have used these HPM files as the basis for our performance calculations. Flop counts for N-atom/unit cell runs on parallel machines are simply multiples of N times those in the HPM file.
The following J90 HPM output file is for bcc Fe using one atom(node)/unit cell in a spin canted mode and using a LIZ size of 3-shells (LIZ27 run).
STOP executed at line 1917 in Fortran routine 'LSMS_MAIN' CPU: 565.730s, Wallclock: 571.738s, 8.2% of 12-CPU Machine Memory HWM: 2670788, Stack HWM: 309171, Stack segment expansions: 0 Group 0: CPU seconds : 565.73 CP executing : 113146019958 Million inst/sec (MIPS) : 23.14 Instructions : 13092927423 Avg. clock periods/inst : 8.64 % CP holding issue : 77.17 CP holding issue : 87312445274 Inst.buffer fetches/sec : 0.18M Inst.buf. fetches: 103548249 Floating adds/sec : 51.82M F.P. adds : 29318632672 Floating multiplies/sec : 50.21M F.P. multiplies : 28405760281 Floating reciprocal/sec : 0.02M F.P. reciprocals : 13974472 Cache hits/sec : 0.34M Cache hits : 192280416 CPU mem. references/sec : 42.71M CPU references : 24160992886 Floating ops/CPU second : 102.06M
The following J90 HPM output file is for bcc Fe using one atom(node)/unit cell in a spin canted mode and using a LIZ size of 6-shells (LIZ65 run).
STOP executed at line 1917 in Fortran routine 'LSMS_MAIN' CPU: 2292.714s, Wallclock: 3321.457s, 5.8% of 12-CPU Machine Memory HWM: 6199197, Stack HWM: 308971, Stack segment expansions: 0 Group 0: CPU seconds : 2292.71 CP executing : 458542950462 Million inst/sec (MIPS) : 13.01 Instructions : 29837135471 Avg. clock periods/inst : 15.37 % CP holding issue : 85.00 CP holding issue : 389741295277 Inst.buffer fetches/sec : 0.13M Inst.buf. fetches: 308476019 Floating adds/sec : 70.45M F.P. adds : 161512383929 Floating multiplies/sec : 69.32M F.P. multiplies : 158939431931 Floating reciprocal/sec : 0.01M F.P. reciprocals : 16386900 Cache hits/sec : 0.13M Cache hits : 305149179 CPU mem. references/sec : 47.96M CPU references : 109954905270 Floating ops/CPU second : 139.78M
High Performance First Principles Method for Magnetic Properties: Breaking the Tflop Barrier
This document was generated using the LaTeX2HTML translator Version 96.1-beta (Jan 15, 1996) Copyright © 1993, 1994, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
The command line arguments were:
latex2html -split 0 index.
The translation was initiated by on Fri Jun 11 11:52:26 EDT 1999