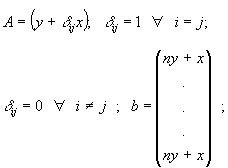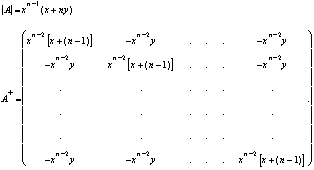Exact Solution of Linear System of Equations Using Chinese Remainder
Theorem
Héctor Eduardo González
División de Estudios de Postgrado de la Facultad de Ingeniería
Doctorado en Investigación de Operaciones
Universidad Nacional Autónoma de México
heg53@prodigy.net.mx
Enrique Cruz Martinez
Dirección General de Servicios de Cómputo Académico
Jefe del Depto. de Supercómputo
Universidad Nacional Autónoma de México
ecm@labvis.unam.mx
Abstract
A parallel code using automatic and OpenMp implementations for solving linear system of equations with integers coefficients (A and b) is presented. The vector solution is obtained by "Chinese Remaind Theorem" without flops operations. This algorithm can be extended to system of equations with real coefficients and the same algebraical structure.
- Introduction
We have solving a linear system of equations with a dense integer coefficient matrix using the direct Gauss – Jordan method and non Euclidean arithmetic with very old background which served us to solve the linear system of equations exactly, without numeric error and without any operation of floating point in a supercomputer.
The way in which the application of a so modern computing tool was conceived for solving an old problem was adjusted to the mathematical process described by the following graph
|
Search of Pattern |
|
Abstraction |
|
Theorizing |
|
Proof |
|
Application |
- Algebraical Structure
Modular Arithmetic is an unusually versatile tool discovered by K.F.Gauss (1777-1855) in 1801. Two numbers a and b are said to be equal or congruent modulo N if N|(a-b), i.e. if their difference is exactly divisible by N. Usually (and on this paper) a,b, are nonnegative and N a positive integer. We write a 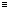 b (mod N).
b (mod N).
The set of numbers congruent to a modulo N is denoted [a]N. If b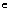 [a]N then, by definition, N|(a-b) or, in other words, a and b have the same remainder of division by N. Since their are exactly N possible remainders of division by N, there are exactly N different sets [a]N.
[a]N then, by definition, N|(a-b) or, in other words, a and b have the same remainder of division by N. Since their are exactly N possible remainders of division by N, there are exactly N different sets [a]N.
Quite often these N sets are simply identified with the corresponding remainders: [0]N = 0, [1]N = 1,..., [N-1]N = N-1. Remainders are often called residues; accordingly, [a]'s are also know as the residue classes.
It's easy to see that if a 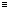 b (mod N) and c
b (mod N) and c 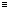 d (mod N) then (a+c)
d (mod N) then (a+c) 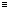 (b+d) (mod N). The same is true for multiplication. These allows us to introduce an algebraic structure into the set {[a]N: a=0,1,...,N-1}:
(b+d) (mod N). The same is true for multiplication. These allows us to introduce an algebraic structure into the set {[a]N: a=0,1,...,N-1}:
By definition:
- [a]N + [b]N = [a + b]N
- [a]N x [b]N = [a x b]N
Subtraction is defined in an analogous manner:
[a]N - [b]N = [a - b]N
and it can be verified that thus equipped set {[a]N: a=0,1,...,N-1} becomes a ring with commutative addition and multiplication.
Division can't be always defined. To give an obvious example:
[5]10 * [1]10 = [5]10 * [3]10 = [5]10 * [5]10 = [5]10 * [7]10 = [5]10 * [9]10 = [5]10.
So [5]10/[5]10 could not be defined uniquely.
We also see that:
[5]10 * [2]10 = [5]10 * [4]10 = [5]10 * [6]10 = [5]10 * [8]10 = [5]10 * [0]10 = [0]10.
something we never had either for integer or real numbers.
The situation improves for prime N's in which case division can be defined uniquely.
Observe multiplication tables below for prime N. For multiplication and division Table We have removed 0 column and row.
Every row (and column) contains all non-zero remainders mostly messed up. So every row is a permutation of the first row in the table. This provides an easy way to construct division tables too. For prime N, the set {[a]N: a=0,1,...,N-1} is promoted to a field.
Table N=5
Addition
|
0 |
1 |
2 |
3 |
4 |
|
0 |
0 |
1 |
2 |
3 |
4 |
|
1 |
1 |
2 |
3 |
4 |
0 |
|
2 |
2 |
3 |
4 |
0 |
1 |
|
3 |
3 |
4 |
0 |
1 |
2 |
|
4 |
4 |
0 |
1 |
2 |
3 |
Subtraction
|
0 |
1 |
2 |
3 |
4 |
|
0 |
0 |
1 |
2 |
3 |
4 |
|
1 |
4 |
0 |
1 |
2 |
3 |
|
2 |
3 |
4 |
0 |
1 |
2 |
|
3 |
2 |
3 |
4 |
0 |
1 |
|
4 |
1 |
2 |
3 |
4 |
0 |
Multiplication
|
1 |
2 |
3 |
4 |
|
1 |
1 |
2 |
3 |
4 |
|
2 |
2 |
4 |
1 |
3 |
|
3 |
3 |
1 |
4 |
2 |
|
4 |
4 |
3 |
2 |
1 |
Division
|
1 |
2 |
3 |
4 |
|
1 |
1 |
2 |
3 |
4 |
|
2 |
3 |
1 |
4 |
2 |
|
3 |
2 |
4 |
1 |
3 |
|
4 |
4 |
3 |
2 |
1 |
For non prime N, most rows contain zeros and repeated entries.
The tables exhibit a variety of patterns. To mention a few
a) For addition, consecutive rows result from the first one by circular rotation of entries.
b) Addition and multiplication tables are symmetric with respect to the main diagonal (it's the one that goes from the top left to the bottom right corner.)
c) Subtraction tables are not symmetric but the rows are still obtained from the first one by rotation of entries. (We subtract numbers in the leftmost column from the numbers in the topmost row.)
d) In multiplication tables, the last row is always a reverse of the first row.
e) In multiplication tables modulo N, rows corresponding to numbers coprime with N contain permutations of the first row.
f) For prime (N+1), multiplication tables offer multiple and simultaneous solutions to the rook problem: on an NxN board position N rooks so that none may capture another. To solve, select a digit, replace all its occurrences with a rook, remove all other digits.
g) Under the same conditions, 1 always appears in the upper left and lower right corners and nowhere else on the main diagonal.
h) 6/5 = 4 (mod 7) or, which is the same, [6]7/[5]7 = [4]7
i) One can use addition and subtraction tables to play the same game as with the Calendar tables.
j) For multiplication tables, this is also true provided selected entries are multiplied instead of being added up.
k) For multiplication tables, both diagonals are palindromic: each is the same both directions.
l) If an addition table has an odd number of rows, then every remainder occurs on the main diagonal.
m) In subtraction tables with an odd number of rows, the second diagonal is a permutation of the first row.
n) In addition tables with an even number of rows, the main diagonal contains only a half of all the remainders. The remainders on the diagonal appear twice each.
o) In multiplication tables with a number of rows N where (N+1) is prime, the same is also true: the main diagonal contains only a half of all the remainders. The remainders on the diagonal appear twice each.
p) In the table of multiplication by N, rows corresponding to the numbers coprime with N consist of permutations of the first row. The reverse is always wrong.
3. Chinese Remainder Theorem
According to D.Wells, the following problem was posed by Sun Tsu Suan-Ching (4th century AD):
There are certain things whose number is unknown. Repeatedly divided by 3, the remainder is 2; by 5 the remainder is 3; and by 7 the remainder is 2. What will be the number?
Oystein Ore mentions another puzzle with a dramatic element from Brahma-Sphuta-Siddhanta (Brahma's Correct System) by Brahmagupta (born 598 AD):
An old woman goes to market and a horse steps on her basket and crashes the eggs. The rider offers to pay for the damages and asks her how many eggs she had brought. She does not remember the exact number, but when she had taken them out two at a time, there was one egg left. The same happened when she picked them out three, four, five, and six at a time, but when she took them seven at a time they came out even. What is the smallest number of eggs she could have had?
Problems of this kind are all examples of what universally became known as the Chinese Remainder Theorem. In mathematical parlance the problems can be stated as finding n, given its remainders of division by several numbers m1,m2,...,mk:
n = n1 (mod m1)
n = n2 (mod m2)
...
n = nk (mod mk)
The modern day theorem is best stated with a couple of useful notations. For non-negative integers m1,m2,...,mk, their greatest common divisor is defined as:
gcd(m1,m2,...,mk) = max{s: s|mi, for i=1,...,k},
where, as always, "s|m" means that s divides m exactly. The least common multiple of k numbers is defined as
lcm(m1,m2,...,mk) = min{s: s>0 and mi|s, for i=1,...,k},
Both gcd() and lcm() are symmetric functions of their arguments. They are complementary in the sense that, for k = 2, gcd(m1,m2)lcm(m1,m2) = m1m2.
However, for k>2 a similar identity does not in general hold. For an example, consider two triplets: {2,4,16} and {2,8,16}. Both have exactly the same gcd and lcm but obviously different products. On the other hand, both gcd and lcm are associative:
gcd(m1, (gcd(m2, m3)) = gcd(gcd(m1, m2), m3)
and, both equal gcd(m1, m2, m3).
Similarly,
lcm(m1, (lcm(m2, m3)) = lcm(lcm(m1, m2), m3)
Associativity allows one to proceed a step at a time with an inductive argument without putting all eggs into a basket at once. Jumping at the opportunity I'll prove the most basic case of k=2.
Theorem
Two simultaneous congruences n 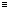 n1 (mod m1) and n
n1 (mod m1) and n 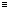 n2 (mod m2) are only solvable when n1
n2 (mod m2) are only solvable when n1 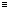 n2 (mod gcd(m1,m2)). The solution is unique modulo lcm(m1,m2).
n2 (mod gcd(m1,m2)). The solution is unique modulo lcm(m1,m2).
When m1 and m2 are coprime their gcd is 1. By convention, a 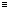 b (mod 1) is simply understood as the usual equality a = b.
b (mod 1) is simply understood as the usual equality a = b.
Proof
The first congruence is equivalent to n = tm1 + n1, the second to n = sm2 + n2, for some integers t and s.
Equating we get
(1) tm1 - sm2 = n2 - n1.
The left-hand side is divisible by gcd(m1,m2). So, unless the right-hand side is also divisible by gcd(m1,m2), there couldn't possibly exist t and s that satisfy the identity.
Now let's assume that gcd(m1,m2)|(n2 - n1) and denote n0 = (n2 - n1)/gcd(m1,m2). Then, (1) can be written as
(2) t(m1/gcd(m1,m2)) = n0 (mod (m2/gcd(m1,m2)))
By definition, m1/gcd(m1,m2) and m2/gcd(m1,m2) are coprime; for we divided m1 and m2 by their largest common factor. Therefore, by a generalization of the Euclid's Proposition, (2) has a solution. Given t, we can determine n = tm1 + n1. These proves the existence part.
To prove the uniqueness part, assume n and N satisfy the two congruences. Taking the differences we see that
(3) N-n = 0 (mod m1) and N-n = 0 (mod m2)
which implies N-n = 0 (mod lcm(m1,m1)).
Let's now solve the two problems we started this section with.
Problem # 1
Solve
p1: x = 2 (mod 3)
p2: x = 3 (mod 5)
p3: x = 2 (mod 7)
From p1, x = 3t + 2, for some integer t. Substituting this into p2 gives 3t = 1. Looking up 1/3 in the division table modulo 5, this reduces to a simpler equation
p4: t = 2 (mod 5)
which, in turn, is equivalent to t = 5s + 2 for an integer s. Substitution into x = 3t + 2 yields x = 15s + 8. This now goes into p3: 15s + 8 = 2 (mod 7). Casting out 7 gives s = 1 (mod 7). From here, s = 7u + 1 and, finally, x = 105 u + 23.
Note that 105 = lcm(3,5,7). Thus we have solutions 23, 128, 233, ...
Problem # 2
Solve
q1: x = 1 (mod 2)
q2: x = 1 (mod 3)
q3: x = 1 (mod 4)
q4: x = 1 (mod 5)
q5: x = 1 (mod 6)
q6: x = 0 (mod 7)
With the experience we acquired so far, the combination of q1-q5 is equivalent to
q7: x = 1 (mod 60)
x = 60t + 1. Plugging this into q6 gives 60t = -1 (mod 7). Casting out 7 simplifies this to 4t = 6 (mod 7) and then 2t = 3 (mod 7). From division tables modulo 7, 3/2 = 5 (mod 7). Therefore, t = 7u + 5. Finally, x = 420u + 301. Allowing for an average size farmer, the most likely number of eggs she might expect to be compensated for is 301.
4. Results
We have proposing this condition to solve a Linear System of Equations using Multimodular Arithmetic
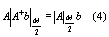
Where 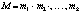 is the composite module,
is the composite module, 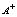 is the adjoint matrix,
is the adjoint matrix, 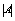 is the determinant and
is the determinant and 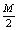 is the symmetrical module.
is the symmetrical module.
With this mathematical condition we found the minimal bound of the prime module which solve the system linear of equations.
We use the matrix
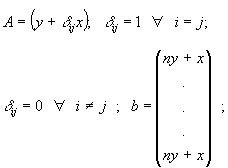
We can to know the value of the determinant and the adjoint matrix
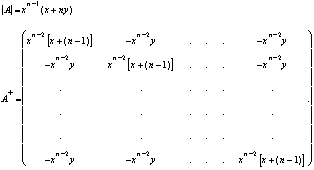
We use a system of the form Ax=b with A generated by the previous matrix with parameters 
The program was writen in the style of FORTRAN 77 and using some intrinsical subroutines of the new standard FORTRAN 90. This code was tested in an Origin 2000 in the Supercomputing Center at UNAM.
For the experiments that we have made we use diferents sizes of the system linear of equations: N=1000,2000 and 5000 and we use from one to six processors (PE's).
The next tables shown the wall times and speed-ups for to obtain the solution using the Chinese Remainder Theorem.
|
Table 1
Timing results (in seconds) for the solution of the system
Ax=b |
|
Size of the System
N=1000 |
|
No. PE's |
Wall Clock(s) |
|
1 |
149.14 |
|
2 |
74.55 |
|
4 |
39.94 |
|
6 |
29.49 |
|
|
Table 2
Speed-up (s) of the solution of the system
Ax=b |
|
Size of the System
N=1000 |
|
No. PE's |
Speed-up (s) |
|
1 |
1 |
|
2 |
2.000 |
|
4 |
3.691 |
|
6 |
4.998 |
|
|
|
Table 3
Timing results (in seconds) for the solution of the system
Ax=b |
|
Size of the System
N=2000 |
|
No. PE's |
Wall Clock(s) |
|
1 |
667.17 |
|
2 |
305.31 |
|
4 |
156.65 |
|
6 |
109.37 |
|
|
Table 4
Speed-up (s) of the solution of the system
Ax=b |
|
Size of the System
N=2000 |
|
No. PE's |
Speed-up (s) |
|
1 |
1 |
|
2 |
2.186 |
|
4 |
4.258 |
|
6 |
6.100 |
|
|
|
Table 5
Timing results (in seconds) for the solution of the system
Ax=b |
|
Size of the System
N=5000 |
|
No. PE's |
Wall Clock(s) |
|
1 |
10167.72 |
|
2 |
5174.41 |
|
4 |
2580.64 |
|
6 |
1735.40 |
|
|
Table 6
Speed-up (s) of the solution of the system
Ax=b |
|
Size of the System
N=5000 |
|
No. PE's |
Speed-up (s) |
|
1 |
1 |
|
2 |
1.965 |
|
4 |
3.937 |
|
6 |
5.859 |
|
|
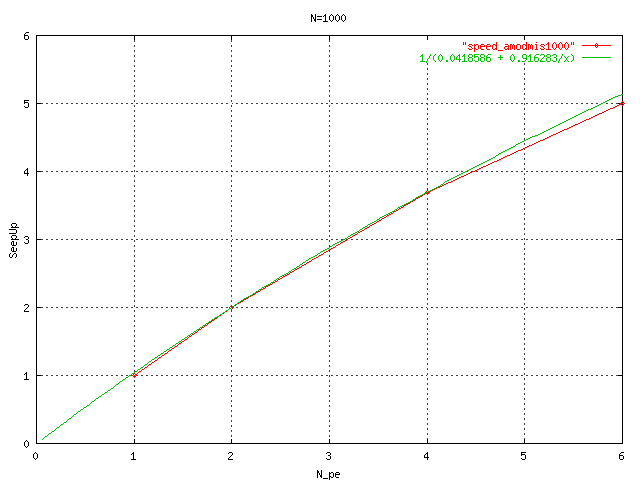
Figure 1 |
|
The speed-up curve for the size N=1000 and the Amdhal Law for this problem |
|
|
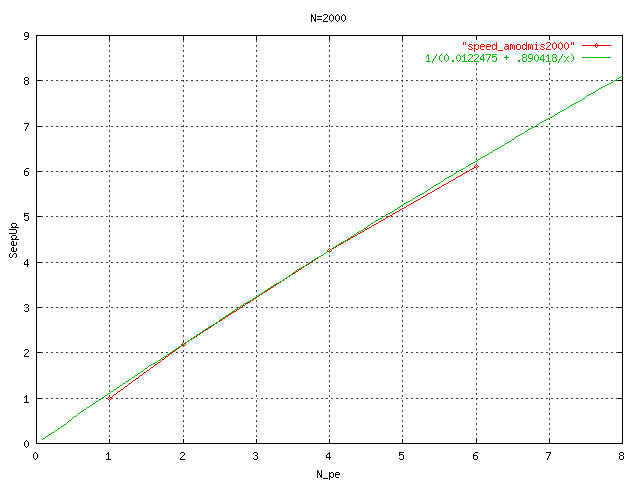
For to measure the Scalability of the algorithm, we calculate the theorical Speep-up using the some mixture of Amdhal Law and 2 experimental data for to obtain the curve for the particular size of the the problem. Next the graphics of the 3 experiments using the Chinese Remainder Theorem.
|
Figure 2 |
|
The speed-up curve for the size N=2000 and the Amdhal Law for this problem |
|
|
|
Figure 3 |
|
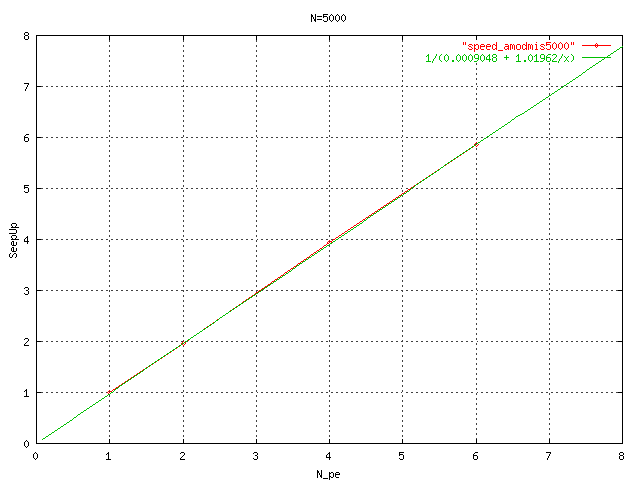
The speed-up curve for the size N=5000 and the Amdhal Law for this problem |
|
|
5. Conclusions
Better utilization of available routines to solve a system linear of equations is always preferred to use other one.
However, a direct solution method should be used if the matrix is dense and non-structured. Further, if the matrix/right side elements of a system linear of equations are integers and a flawless solution is desired, this multimodular arithmetic must be used.
For this kind of problems we observe a behavior very close to ideal speedup, in the case of N=2000 we observe a superlinear speedup.
In any case this problem with the dense matrix and the easy decomposition of the problem in terms of tasks, and the tasks make some calculation using a module it is very parallel.
6. References
J.H.Conway and R.K.Guy, The Book of Numbers, Springer-Verlag, NY, 1996.
H.Davenport, The Higher Arithmetic, Harper&Brothers, NY
K.Devlin. Mathematics: The Science of Patterns, Scientific American Library, 1997
R.Graham, D.Knuth, O.Potashnik, Concrete Mathematics, 2nd edition, Addison-Wesley, 1994.
P.Hilton, D.Holton, J.Pederson, Mathematical Reflections, Springer Verlag, 1997
Oystein Ore, Number Theory and Its History, Dover Publications, 1976
S.K.Stein, Mathematics: The Man-Made Universe, 3rd edition, Dover, 2000.
H.Davenport, The Higher Arithmetic, Harper&Brothers, NY
P.J.Davis and R.Hersh, The Mathematical Experience, Houghton Mifflin Company, Boston, 1981
R.Graham, D.Knuth, O.Potashnik, Concrete Mathematics, 2nd edition, Addison-Wesley, 1994.
Oystein Ore, Number Theory and Its History, Dover Publications, 1976
D.Wells, The Penguin Book of Curious and Interesting Puzzles, Penguin Books, 1992
Golub, G.H., Van Loan, Ch. F.Matrix Computations.Jhon Hopkins University Press.1983.
Davenport,J.H.,Siret, Y., Tournier, E.Computer Algebra. Systems and Algorithms for Algebraic Computations. Academic Press. 1988.
Grosswald,E.Topics from the Theory of Numbers Mc Millan Company, N.Y.1966.
Young, David M.; Gregory, Robert Todd. A Survey of Numerical Mathematics. Volumen II. Dover Publications, Inc., 1972.