Probing the universe via an intercontinental cluster of T3Es

In this paper we describe a novel use of metacomputing, the processing of data from an experimental facility. We use phase-coherent de-dispersion techniques to search for pulsar candidates in observational data acquired at the 76-m Lovell radio telescope. A software-based pulsar search of this kind offers advantages over similar hardware-based methods; hitherto such methods have generally been eschewed because of the high demands they make on computing resources. Our method is pleasingly parallel and has a high ratio of computation to communication, which facts make it viable in a metacomputing environment, yet raises interesting challenges nonetheless.

At the Supercomputing 99 conference, we demonstrated our method as part of an award-winning set of metacomputing experiments, which linked together Cray-T3E systems in the UK, Germany, and the USA, with an Hitachi SR8000 in Japan. In contrast to the demonstrations of our collaborators [1,2], our data-intensive application is limited by communications bandwidth rather than latency. This presents particular challenges since the movement of the data around the metacomputer makes severe demands on the intercontinental bandwidth.

The remainder of the paper is structured as follows. Section 2 describes the application in more detail. Section 3 outlines how the application was adapted to a metacomputing environment. Section 4 describes the configuration of the metacomputer and underlying network as used in the SC99 demonstrations. In section 5, we motivate the idea of processing experimental data in near real-time, and discuss work in progress to achieve this. Section 6 rounds off the paper.

Phase-coherent De-dispersion and Pulsar Searches

Pulsars are rapidly-rotating, highly-magnetised neutron stars, emitting beams of radio waves which permit the detection of characteristic, regularly-spaced "pulse profiles" by radio telescopes on the Earth's surface. The fastest pulsars have rotational periods of only a few milliseconds, and, as massive, essentially frictionless flywheels, make superb natural clocks. These millisecond pulsars permit a wide variety of fundamental astrophysical and gravitational experiments. Examples include the study of neutron stars, the interstellar medium and binary system evolution, and stringent tests of the predictions of general relativity and cosmology.

The observed radio signal from pulsars manifests itself at the telescope as a periodic increase in broadband radio noise. It order to observe the pulse with a high signal to noise ratio we need to observe across a wide band of radio frequencies. As the space between the earth and the pulsar (the interstellar medium) is slightly charged it is dispersive and therefore different frequencies propagate at different velocities. The practical result of this effect is that the pulse is detected at the high frequency end of the band before it arrives at the low frequency end. If do not correct for this propagation effect the pulse profile is not observable as it is broadened by this "dispersive delay" The amount of broadening a particular pulsar observation will display is related directly to our distance from the pulsar and the charge density along the signal path and is characterised by the dispersion measure or DM.

The University of Manchester Radio Astronomy group at Jodrell Bank has built a data acquisition system designed to remove completely these dispersive effects by applying a software filter to digitally recorded signals from the 76-m Lovell telescope. This method, known as phase-coherent de-dispersion, is very effective and flexible, but it is also computationally intensive and therefore difficult to apply routinely.

The application of this method is simple. The action of the interstellar medium is actually the same as applying a frequency dependent filter which retards the phase of the propagating radio signals. We can therefore remove the effects by convolving the observations with the inverse of this filter. This method completely removes the dispersive effects but requires that we know the DM of the pulsar in order to correctly construct the inverse filter. In most cases the DM is well determined but if we wish to search for new pulsars with unknown DMs we have to apply many trial filters which is generally considered to be computationally impractical.

We have applies this method to the problem of searching for new pulsars in globular clusters. Globular clusters are spherically symmetric, gravitationally bound collections of from tens of thousands to millions of stars, which all formed at approximately the same time. The fact that they are clusters of stars at approximately the same distance from the earth means the DM of any pulsars in the cluster would fall within a narrow range. We can also get an independent estimate of the DM of the cluster using a model of the galactic electron distribution. These two facts combine to allow a small number of trial DMs to be used and therefore globular clusters are ideal candidate areas for this system to search.

The de-dispersion proceeds by firstly breaking the data up into lengths which have to be of length at least twice of the dispersive delay time across the observing bandwidth. Each length is then subjected to a Fourier transform and multiplied by the Fourier transform of the inverse filter. The resultant data length is then transformed back into the time domain and processed to produce a de-dispersed time series. The next length is then processed, the resultant series are then concatenated together. In practical terms the input data-set only has to be forward transformed once, but has to transformed back into the time domain as many times as we have trial DMs.

The result of the de-dispersion is a time series for each trial dispersion measure. These time series are then subject to various analytical methods whose aim is to determine the presence of periodic signals. This analysis produces a list of candidate periods which may be pulsars or local radio interference, or simply may be artifacts of the data collection hardware and subsequent software processing. These candidates can then confirmed or rejected by further observations.

The original de-dispersion code was already parallelized for a single Cray-T3E, in the simplest manner imaginable. Each PE was allocated a contiguous segment of the global time series, and was responsible for reading its own data from disk. MPI was only used to determine the rank and size information necessary to share the data amongst processors. It is this embarrassing level of parallelism that makes the application well suited for running on a metacomputer.

Implementation on the metacomputer

Our aim was to adapt the de-dispersion code to a metacomputing environment in which the input data resides on one Cray-T3E, the local host, and processors on remote Cray-T3Es are enlisted to reduce the turnaround time. This required

Of these, the first required some degree of code restructuring but was otherwise straightforward. Our methods for satisfying the other requirements are described later in this section.

It should be noted that the application is extremely data intensive - a few minutes of observations produces several Gigabytes of data - and the factor limiting our ability to utilise remote processors is therefore the network bandwidth to remote hosts. In fact, running the pulsar search code on less than 50 dispersion measures during the SC99 demonstrations would not have been viable.

PACX-MPI

PACX-MPI (PArallel Computer eXtension) [4,5] is an on-going project of the HLRS, Stuttgart.¹ It enables an MPI application to run on a metacomputer consisting of several, possibly heterogeneous, machines, each of which may itself be massively parallel.

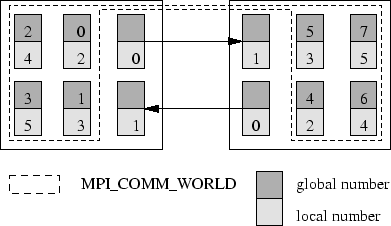
From the programmer's point of view, the PACX-MPI approach is very convenient. Provided that the programmer does not step outside the bounds of the (increasingly) large subset of MPI-1.2 that PACX-MPI supports, a correct and portable MPI application can be expected to compile and run without alteration under PACX-MPI. The application code sees a single MPI_COMM_WORLD consisting of processes on all hosts.

PACX-MPI achieves this by reserving an additional two processes on each host to mediate inter-host communications. These "daemon processes" are hidden from the application code.² All inter-host communications are routed through these daemon processes, a feature which permits message bundling and minimizes the number of connections between hosts. All intra-host communications are delegated to the host's native MPI library.

Figure 1 illustrates how the processes in local communicators on two systems are combined to form a single MPI_COMM_WORLD. Two processors on each system are hidden from the application code; these serve as daemons for external communication.

**Figure 1:** Process numbering in PACX-MPI - two systems integrated into a single MPI_COMM_WORLD. On each system, processes 0 and 1 in the local numbering act as daemons for external communication; these processes are hidden from the application code.
$\begin{figure} \centerline {\psfig{file=concept.eps,height=5cm}}\end{figure}$

The user defines the metacomputer configuration in a short text file .hostfile, which must be replicated in the working directory of the application on each host. On the local host (the first system listed in the .hostfile), the application is launched via the standard mechanism (eg. mpirun), making provision for the two daemon processes. On remote hosts, PACX-MPI offers two methods for launching the application, automatic or manual.

Of the two, the automatic startup facility is far more convenient. The user provides, in the .hostfile, additional information that the PACX daemons use to start the application on the remote systems. Unfortunately, the automatic startup facility did not work on Cray-T3E systems at the time of SC99; the problem is related to restrictions on spawning processes on application PEs.

In manual mode, the user must manually launch the MPI application on each host. On hosts beyond the first, the socket numbers to use for inter-host communication must be specified in additional command-line arguments.

Diagnosing the metacomputer

In order to make efficient use of a metacomputer in which the MPI bandwidth of inter-host messages is some two orders of magnitude slower than intra-host messages, it is sensible for the application to take account of the network topology. This requires knowing how many hosts are involved and on which host a given processor resides.

Now the MPI specification, which was aimed more at cluster environments or single MPPs than metacomputers made up of multiple MPPs, does not provide a function for this specific purpose. Moreover, PACX-MPI adopts the defensible policy of not providing any extensions to MPI. It is therefore up to the application developer to find a solution.

One possibility, advocated by the PACX development team, is to abuse the MPI function MPI_Get_processor_name, which promises to return a unique string for each processor in MPI_COMM_WORLD; although this can be made to work in most cases, the MPI specification does not prescribe the format of the resulting string, a fact which detracts from the method's generality.

A second possibility is to have one processor, the obvious choice being rank 0 in MPI_COMM_WORLD, read and parse the .hostfile. This is unattractive for several reasons, not the least being that the source code becomes dependent on the flavour of MPI.

The method adopted here is specific to Cray-T3E systems. It relies on the fact that the Cray-T3E implementation of MPI_Comm_rank returns ranks in MPI_COMM_WORLD that match the return value of the Cray-T3E intrinsic my_pe(), and on the fact that the local ordering of ranks within a host is preserved in the PACX-MPI global ordering. Each process calls my_pe(), the results are gathered into an array, and host boundaries are identified by traversing the array in ascending rank order.

Parallelization strategy

The original intention was to adopt a master-slave model in which one (or more) master processes read the disk and distribute work to slave processes. This approach is attractive because it naturally furnishes an effective method of load-balancing. However, we require each processor to get maximally contiguous chunks of the global time series, and this added a complexity that we were reluctant to tackle head on in the few weeks we had available for the entire project.

The second alternative considered, and the one ultimately adopted, minimized the impact on the code. We allocate a single, contiguous portion of the global time series to each worker, and make each worker keep track of its position, just as in the original code. What we have now is essentially a client-server model. A handful of server nodes poll for requests for data from clients, and the bulk of intelligence resides within the clients who do the actual work.

In fact, the code executed by the client nodes is very little changed from the code originally executed by all processors. The main impact is in the routine which previously accessed the disk. Instead, the client sends a request for specific to its allocated server, and awaits the reply. When the client has finished its allocated work, it sends a special sign-off message to its server. When a server receives a request for data from a client, it opens the appropriate file if necessary, seeks to the correct position, performs the read, then sends the message to the client. Each server keeps a count of active clients, and continues polling for requests until this count is reduced to zero when the last client signs off.

One disadvantage of the client-server model adopted here is that we are compelled to tackle the load-balancing problem statically, taking into account estimates of the MPI bandwidth, processor speed, disk performance and so on. The algorithm used is described below in general terms to permit the analysis to be extended to metacomputing clusters of differing numbers and types of host machines.

Static Load Balancing

Let $N_{\rm hosts}$ be the number of hosts, and let $n_{i}$ be the number of client processors to use on host

, discounting the extra 2 processors required by PACX-MPI and those processors on host

which have been assigned to server duties. Denote the bandwidth, in megabytes/sec, from host 1 (where the input data resides) to host

by ${\beta}_{i}$ . The rate, in megabytes/sec at which data can be read from disk on host

is denoted by

; it is assumed that this rate is approximately independent of the number of processors accessing the disk at any one time.

The size of one record is denoted by

. The computational time required to process one record of data on host 1 is determined experimentally and denoted by $\tau$ . The time to process the same quantity of data on other hosts is estimated by multiplying $\tau$ by the ratio $p_{1}:p_{i}$ where $p_{i}$ is the peak speed in Mflops of the processors on host

.³ This approximation is justified in a homogeneous metacomputer, but is likely to overestimate (underestimate) slightly the compute time on processors slower (faster) than those of host

In the search version of the code, $n_{\rm slopes}$ is the number of slopes (dispersion measures) to be analysed. $\tau$ is now to be re-interpreted as the average compute time per record per unit slope in the regime where $n_{\rm slopes}$ is large enough that the compute time per megabyte can be well approximated by $\tau \times n_{\rm slopes}$ .⁴

Any job will process a total of

records. The load balancing problem is to determine the proportion

$\begin{displaymath} v_1 : \ldots : v_n, \hspace{1cm} \sum_{i=1}^{N_{\rm hosts}} v_i = v \end{displaymath}$

(1)

$\begin{displaymath} t_i = \frac{v_i}{n_{i}} t_{\rm proc}\left(i\right) + n_{i} t_{\rm wait}\left(i\right) \end{displaymath}$

(2)

$\begin{displaymath} t_{\rm wait}\left(i\right) = \left( \frac{w}{{\beta}_{i}} + \frac{w}{r} \right) \end{displaymath}$

(3)

$\begin{displaymath} t_{\rm proc}\left(i\right) = n_{\rm slopes}\tau \frac{p_{1}}{p_{i}} \end{displaymath}$

(4)

The first term on the right hand side of equation (2) is the time required for computation. The second term is essentially twice the start-up time, ie. the time elapsed until all processors on the host have received their first work unit. This term will be dominated by communications bandwidth on remote hosts and by disk access speed on the local host. A similar cost is paid at the end ( run-down time) as some processors will finish their allocated work before others.

The condition used to balance the work load is that all hosts finish at the same time.

$\begin{displaymath} t_1 = t_2 = \ldots = t_{N_{\rm hosts}} \end{displaymath}$

(5)

Using equation (5) in equations (2) and (1) leads to a linear system with $N_{\rm hosts}+ 1$ equations and $N_{\rm hosts}+ 1$ unknowns $(v_1, \ldots, v_{N_{\rm hosts}}, t)$ .

$\begin{displaymath} \left( \begin{array}{ccccc} a_1 & 0 & \cdots & 0 & -1 \\ 0 ... ... \\ b_2 \\ \vdots \\ b_{N_{\rm hosts}} \\ v \end{array}\right) \end{displaymath}$

(6)

$\begin{displaymath} a_i = \frac{\tau }{n_{i}} \frac{p_{1}}{p_{i}} \end{displaymath}$

(7)

$\begin{displaymath} b_i = n_{i} w \left( \frac{w}{{\beta}_{i}} + \frac{w}{r} \right) \end{displaymath}$

(8)

The validity of this method depends on the implicit assumption that no client processor experiences dead time waiting for other clients to receive their data. A global condition which expresses this is the inequality

$\begin{displaymath} t_i > v_i \left( \frac{w}{{\beta}_{i}} + \frac{w}{r} \right). \end{displaymath}$

(9)

$\begin{displaymath} t_{\rm else}\left(i\right) = \left(n_{i}-1\right) t_{\rm wait}\left(i\right) \end{displaymath}$

(10)

as the time that it takes all the other processors on host

to receive their work units. Then

$\begin{displaymath} t_{\rm dead}\left(i\right) = \left\{ \begin{array}{ll} t_{\... ...left(i\right) \\ 0 \quad \mbox{otherwise} \end{array} \right. \end{displaymath}$

(11)

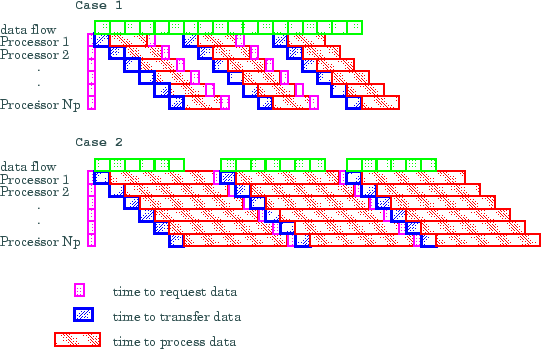
Figure 2 illustrates this graphically. In case 1, remote client processors experience dead time between work units. This dead time can be reduced by improving the bandwidth, reducing the number of remote clients, and/or increasing $n_{\rm slopes}$ . In case 2, there is sufficient bandwidth to keep the remote clients fully utilised.

**Figure 2:** Data flow. In case 1, each client processor has to wait for other processors to receive their next work units. In case 2, there is no dead time, and client processors are fully utilised.
$\begin{figure} \centerline {\psfig{file=sc99.eps,width=12cm}}\end{figure}$

Our code solves the linear system (6) at run time. No attempt is made to account for dead time in the load balancing, other than to report a warning if any $t_{\rm dead}\left(i\right) > 0$ .⁵ Instead, we calculate in advance the minimum number of processors on each remote host required to saturate the estimated bandwidth to that host, and avoid reserving more processors than can be fully utilised. We have a program, based on the same load balancing routine, to perform the necessary parameter search.

The results $v_1,\ldots,v_{N_{\rm hosts}}$ of the solution of the linear system are, of course, real numbers, yet we can only allocate whole work units. In practice, we allocate a number of work units to host

equal to the largest integer not exceeding

; this integer is divided by $n_{i}$ (in integer arithmetic), each processor gets the quotient and the remainder is distributed in round robin fashion.

Scheduled service

A drawback of the client-server approach, when coupled with the FIFO processing of requests by servers, is that in practice the run-down time is usually longer than the start-up time. The reason is as follows. Typically there are clients on a given host to which is allocated one more work unit than other clients on the same host, but there is no guarantee that the more heavily loaded clients will be served before the others. Consequently, some clients may start their last work unit before other clients have received their penultimate one. These end effects can be expected to be more pronounced when the number of records per client is small, or equivalently, when the start up time is comparable to the total elapsed time. Indeed, this was confirmed in the metacomputing experiments at SC99; the estimates of elapsed time in longer runs with 10 or more 1 Mb records per client were entirely acceptable.

Nonetheless, the excessive run-down times can be eliminated completely by the simple expedient of imposing a schedule on the servers. The remedy has the attractive side effect of eliminating all messages carrying requests from clients to servers along with the associated latency penalties. In hindsight the method seems obvious - given that the distribution of data amongst clients is predetermined, it is not difficult to see that a schedule of messages effecting the data distribution can also be predetermined - yet the idea did not occur to us in time to incorporate it in the version used at SC99.

The Supercomputing 99 demonstrations

Overview of the SC99 global network

During Supercomputing'99 four supercomputers in Europe, the US and Japan were linked together to form a metacomputer.

**Figure 3:** Network configuration as set up during Supercomputing'99.
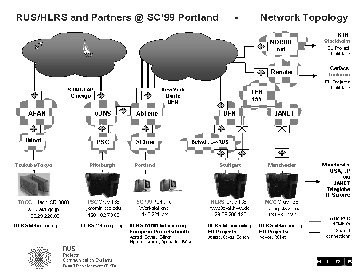$\begin{figure} \centerline {\psfig{file=sc99topo.eps,height=6cm}}\end{figure}$

Details of the network configuration can be seen in figure 3. Using ATM, PVCs were set up with a bandwidth of 10 MBit/s in the European networks. On all other connections bandwidth was shared with other users.

Needless to say, the logistics in setting up this network were formidable, and we remain indebted to all who played a part. Equally formidable was the degree of coordination required among the various supercomputing centres, each of which had to provide interactive access to large numbers of processors at agreed two-hour slots on four successive days; some of the partners (and one of the authors) found themselves working in the middle of the night!

Experiments

Although some of the SC99 experiments made use of the entire metacomputer, the pulsar search code was not one of these. We did not make use of the Hitachi SR8000 for the simple reason that our code was unashamedly T3E specific (notably in the FFT routine). Despite the heroic efforts of network specialists, the intercontinental bandwidth was still too low for our bandwidth-limited application to fully utilize the available remote processors. We aimed instead to use no more remote processors than necessary to saturate the available bandwidth.

Input data, observations of the globular cluster M80, were pre-loaded onto the Cray-T3E in Manchester. Our latest estimates of bandwidth to remote hosts were supplied to the application at run time. The dedicated Manchester-Stuttgart link was observed to sustain an MPI bandwidth of about 0.8 Mbyte/s, with only small fluctuations. The Manchester-Pittsburgh link sustained about 0.5 Mbyte/s for short periods, but large fluctuations in the volume of traffic meant that the bandwidth fell to levels much lower than this. We were forced to revise out estimates of the Manchester-Pittsburgh bandwidth several times during the course of SC99.

We ran four successful experiments during SC99, on the configurations shown in table 1. Note that the full configuration of the metacomputer was only available on the day on which experiment 2 was run.

Two problems and two solutions

The first was that under certain circumstances servers, polling for requests using MPI_Recv with both source and tag wild-carded, intercepted messages associated with a collective operation. This was reported to the PACX-MPI development team, and turned out to be a previously unknown bug in PACX-MPI. As the problem only manifested when all client nodes on a remote host finished while local clients were still occupied, it was possible to avoid the failure by deliberately overestimating the bandwidth to the remote hosts. A more careful work-around was devised and implemented the following day: inserting an extra field in the body of the request message to convey the request type (previously conveyed by the tag), and using the same tag on all request messages, gave sufficient context protection to avoid the problem.

Another unexpected problem was discovered when running with 256 clients on a single remote host - the program failed with insufficient buffer space on the PE responsible for sending data from the local host. The problem is thought to be caused by the fact that, in view of the slow intercontinental bandwidth, available buffer space fills faster than it can be drained. On the day that this problem was discovered, the work-around of reducing the number of client processors on the Stuttgart machine from 256 to 128 was adopted. The problem was cured the following day by changing the code to allocate (at least) one server PE for every 128 clients.

Real-time processing

Work is in progress to enhance the de-dispersion code so that observational data captured at the observatory can be streamed across a high-speed link to the Cray-T3E in Manchester for processing in near real-time. The ability to process data while the observation is in progress is invaluable. Any need for recalibration or intervention can be detected early, thereby avoiding waste of a precious, even unique resource. If the results can be interpreted as they are being produced the experimental regime can be adapted accordingly, again maximizing the usage made of the facility. Furthermore, whether or not the raw observational data is actually stored becomes a matter of choice instead of necessity; in some cases, the additional freedom may enable experimental programmes that would otherwise be prohibitively expensive or simply infeasible.

Introducing real-time processing into the de-dispersion code raises several new issues. The primary objectives are now to ensure that the lag between input data and results is small and non-increasing. The requirement of a small lag compels us to allocate work in the smallest possible units, ie. in single FFT chunks. The requirement that the lag does not increase is equivalent to ensuring that there is sufficient processing power to keep up with the input stream. In contrast to the SC99 demonstrations in which we tried to avoid the dead time that arose out of being able to process data faster than it could be delivered, having spare processing capacity is now preferable to having not enough.

The fact that we are now processing a stream of input data forces a complete revision of our approach to parallelization. In the SC99 demonstration, we had the entire time-series laid out on a direct access storage device, and we could decompose the data into continuous segments and allocate one to each processor; the client-server approach depended on the ability to seek to an arbitrary displacement in the time series. The constraint of processing the time series in a prescribed order turns an embarrassingly parallel problem into something much more challenging.

The approach that we are pursuing can be thought of as a hybrid between master-slave and a two-stage pipeline. The master processor is responsible for reading the input stream and allocating work units to slaves. Slaves can be called upon to do work in either the first or second stage of the pipeline. The first stage involves performing a FFT on a block of data, and then passing the results on to a second stage processor. The second stage involves re-assembly of results received from first stage processors and post-processing on the resultant contiguous chunks. It is the duty of the master to orchestrate the interprocess messages. This is achieved by notifying each slave, as it reports in for instructions, of the rank of the other processor to send results to or receive results from.

Conclusion

We have described the realization of a global metacomputer which comprised supercomputers in Japan, the USA, Germany and the UK. During SC99 the usability of this metacomputer has been demonstrated by several demanding applications, including our own pulsar search code. We have shown that even data-intensive applications, such as processing output from experimental facilities, can be successfully undertaken on such a metacomputer. We have described on-going work to process experimental data in near real-time, thereby enabling more efficient use of the experimental facility and simplifying the data management problem.

We look forward to the day when such techniques become commonplace. Although the emerging "computational grid" promises to deliver the necessary infrastructure and middleware, there are many questions yet to be answered satisfactorily, such as resource co-allocation, resource reservation and guaranteed quality of service. We appeal to vendors to help by building mechanisms for resource reservation into their queueing systems.

Acknowledgments

The authors would like to thank Tsukuba Advanced Computing Center, Pittsburgh Supercomputing Center, Manchester Computing Centre, CSC, High Performance Computing Center Stuttgart, BelWü, DFN, JANET, TEN-155, Abilene, vBNS, STAR-TAP, TransPAC, APAN and IMnet for their support and co-operation in these experiments. The advice of Edgar Gabriel, Matthias Müller and Michael Resch was especially helpful.

References

Footnotes

¹ Further documentation is available on-line at
http://www.hlrs.de/structure/organisation/par/projects/pacx-mpi/

² It is therefore erroneous for a PACX-MPI program to use features such as the Cray-T3E barrier() intrinsic.

³ This assumes that all the processors on any given host are clocked at the same speed, as was the case in the SC99 demonstrations.

⁴ The forward FFT's are computed only once, but the inverse FFT's must be computed for each slope. It should be obvious from this how to repair the approximation for small $n_{\rm slopes}$ .

⁵ Simply absorbing $t_{\rm dead}\left(i\right)$ into $t_{\rm proc}\left(i\right)$ isn't quite right. The number of times that a processor pays the dead time penalty is one less than the number of work units it is allocated, and this quantity depends on