HPF Programming: Myth or Reality?
A User's Point of View
Jean-Yves Berthou
CEA/DI-Cisi
CEA-Saclay, Bat 474
91191 Gif-sur-Yvette cedex, FRANCE
Laurent Colombet
CEA/DI-Cisi
CEA-Grenoble, 17 Rue des Martyrs
38054 Grenoble cedex 9, FRANCE
Abstract
It is now well known that the data parallel programming model significantly speeds up the development time of parallel code compared to the message passing programming model. But, it is also well known that data parallel compilers still have great progress to make in order to be competitive to message passing libraries.
We have implemented, using Craft (the Cray MPP data parallel language) and HPF 1.1, three basic scientific codes and kernels: a weather forecast program from NCAR, a tensor product, a Monte Carlo application. We compare the performance of the HPF programs to their Craft and message passing versions. Then, we discuss the pros and cons of the data parallel compilers we used and HPF data parallel programming[For94] .
1 Introduction
Since 1987, CEA users have developped data parallel codes in order to solve new large-scale problems. The first applications that have been written with CM-Fortran, the data parallel language of the Thinking Machine computer, have produced some interesting results and shown the capabilities of the data parallel model. But the translation of a part of these applications into Craft without even a good efficiency has somewhat discouraged users to write data parallel codes. Moreover, since Craft was a computer-seller language, the Craft codes were not portable. But, it is clear that an efficient and portable data parallel language that allows users to write more easily parallel codes is still needed. The HPF language has become in the past two years a de facto standard for data parallel programming. The recent coming out of industrial commercial HPF compilers reassures end users on the perenniality and viability of HPF programming.
The aim of this paper is to help potential users of data parallel programming to understand the current world of High Performance Fortran (HPF) and to anticipate future developments with it. It is expected that HPF, which combines full Fortran 90 language with special user directives dealing with parallelism, will be a standard programming model for production codes on many types of machines, such as vector processor machines (like Cray T90) and massively parallel computers (like SGI Origin 2000 or Cray T3E). For scientists who wish to take advantage of the power of all computer architectures, the use of HPF seems to be an interesting apportunity.
In the following sections, we study three applications, a weather forecast program from NCAR, a tensor product and a Monte Carlo application, in order to evaluate the capabilities to have good speedup and efficiency using automatic parallelization and the HPF language. The target machines on which we performed the experiments are a Cray T3D with 128 processors and a T3E-600 with 128 processors. The following table summarizes the characteristics of these machines:
Table 1
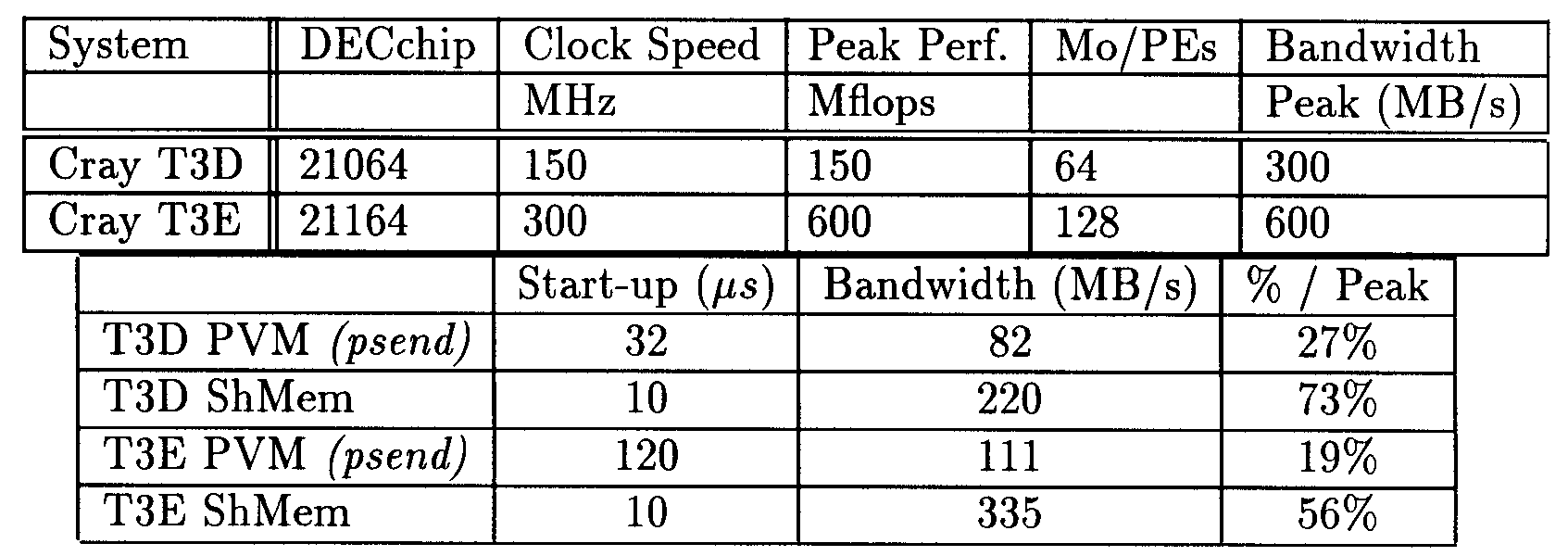
We currently have at our disposal a T3-750 with 256 processors. We briefly present the performance of the Tensrus code on this machine. The data parallel compilers we used are: Craft (Cray T3D proprietary data language), pghpf 2.1 from Portland Group Inc.[TPG96, BMN+97] and xhpf 2.1 from Applied Parallel Research[Res95]. In the following pghpf refers to pghpf2.1 and xhpf refers to xhpf2.1. The conclusion section discusses the pros and cons of the data parallel compilers we used and HPF data parallel programming.
1.1 A Few Words About Data Parallel Programming
A program which performs identical computations over a large set of data points, is called a Data Parallel program. The approach to parallelizing this type of programs consists in distributing the data over the number of available processors. Then, each processor independently performs the computations on its subset of data. Basically, a data parallel programming language supports features (i.e., compiler interpreted keywords) allowing the programmer to specify the data distribution. HPF is currently known as the future standard for Data Parallel programs.
From a default, or user's imposed data distribution, the HPF compiler has to generate an SPMD-type (Single Program Multiple Data) executable that optimally uses an underlying message passing communication protocol for inter-processor data transfers. In the SPMD programming style, all processors execute the same program (i.e. the same instruction set) but on private data only, that is to say the data stored in the local memory of the processor. If a processor needs to access remote data from another processor, the values are transferred using the interconnection network, and stored in the local memory. Most compilers apply the owner computes rule, which states that the processor that will do the computation is the one which owns the data to be modified. A simple implementation of this rule, called run time resolution, can be obtained by a test during the execution of each processor's program to detect whether for each instruction the value to be modified is in its local memory. If this is the case, the instruction will be executed. If a non-local read-only value is needed, there will be a remote load from the processor which holds this value. Of course, the run time resolution technique is inefficient, and generally, compilers use this approach only if they cannot determine at compile time the data points which have to be exchanged among processors and the instructions which have to be executed by each processor.
One technique to hide communication time consists in overlapping communications with computations [CCM95]. Communication is performed while the receiving processor is still computing. A detailed data flow analysis (see [Fea93]) allows the automation of this technique. However, commercial compilers currently make no use of this (or similar) technique(s). The optimization of inter-processor communication is still the key to achieving a fully optimized (i.e., fully scaling) parallel executable. The message vectorization optimization [Ger90] uses the level of loop-carried data dependencies to calculate whether communication may be legally performed at outer loops, replacing many small messages with one larger message. This optimization is one of the most worthwhile. As for message vectorization, most communication optimizations (message coalescing, message aggregation) need at least a full dependence analysis, and at best a data flow analysis.
2 The Shallow Program
The shallow code is a weather forecast program from National Center for Atmospheric Research Boulder. We have retrieved it from the Applied Parallel Research Benchmark suite. This code handles 513 x 513 matrices and is regular and static. Thus, it is a good candidate for automatic parallelization and HPF programming.
We submitted the Fortran 77 version of shallow to the xhpf parallelizing compiler. The sequential execution time on one processor of the Cray T3D MPP was equal to 131.9s. The automatic parallelizer produced a parallel code which had an execution time on a single processor equal to 70 seconds! This improvement is due to the data distribution produced by xhpf, which improves data locality and so decreases cache misses. Some performance measurements with Apprentice (a monitoring tool for the T3D) confirmed this analysis. In the original version, 80% of the computation time is spent in memory access, compared to 35% for the xhpf version.
We produced automatically an HPF version of shallow using xhpf and improved this HPF version in a few hours. The HPF code has been submitted to the pghpf compiler. The following table summarizes the execution times, the efficiency of the parallel program1 and the MFLOPs obtained with the HPF version of shallow executed on Cray T3D and T3E compiled by the pghpf and the xhpf compilers.
Table 2
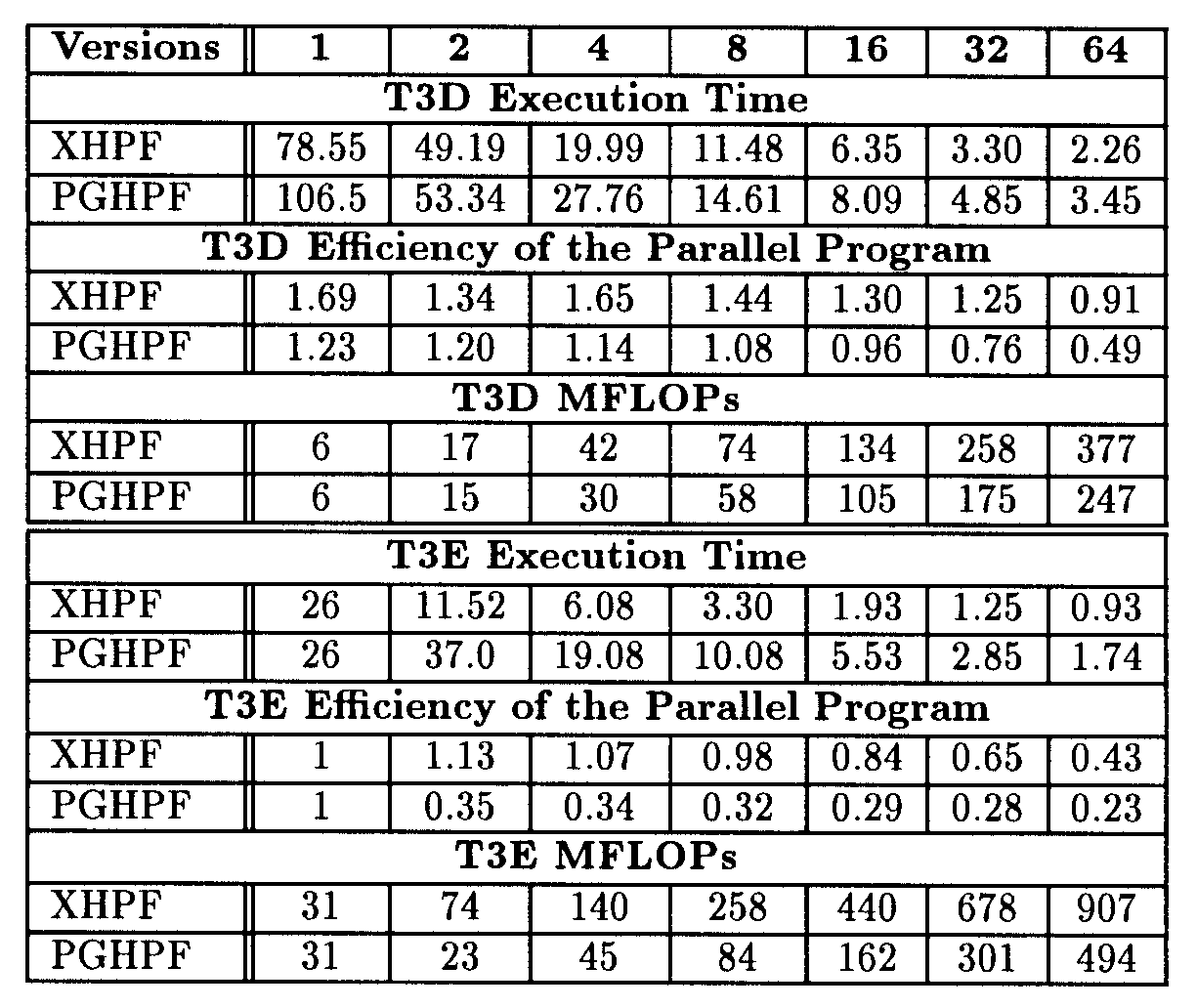
On T3D, xhpf leads to better performance than pghpf does: until 32 processors, xhpf obtains 8-11 MFLOPs/processor while pgphf obtains 4-8 MFLOPs/processor. The ratio T3E/T3D of the execution times is good for xhpf ( 3) while it is very disappointing for pghpf. This clearly, proves that HPF programming is viable but performance is very compiler-dependent.
3 Ising: Simulation of the 2D Ising Model Using the Monte Carlo Method
The ising program simulates the 2D Ising model (2 iterations), using the Monte Carlo method (Metropolis algorithm). The sequential version has been written by Alain Billoire, CEA/DSM/SPHT and handles 512 x 512 matrices. Francois Robin, CEA/DAM, has written a Craft version of ising. We have translated the Craft version into HPF within two days. The HPF code has been sumitted to xhpf and pghpf on T3D and T3E. Unfortunately, xhpf failed in compiling the HPF version. According to the Applied Parallel Research support team, xhpf misinterprets the bi-dimensional data distributions.
The characteristics of the HPF code are the following. The arrays, which are all bi-dimensional, are (block,block) distributed. The two intrinsic functions cshift and sum are intensively invoked.
The experiments we present below were performed on two iterations of the main loop included in the ising program. These two iterations represent 350x106 floating point operations and 600x106 integer point operations. In the following MINTOPs stands for million integer operations per second. As it can be seen in the following table, the performance of the Craft version on T3D was very poor.
Table 3
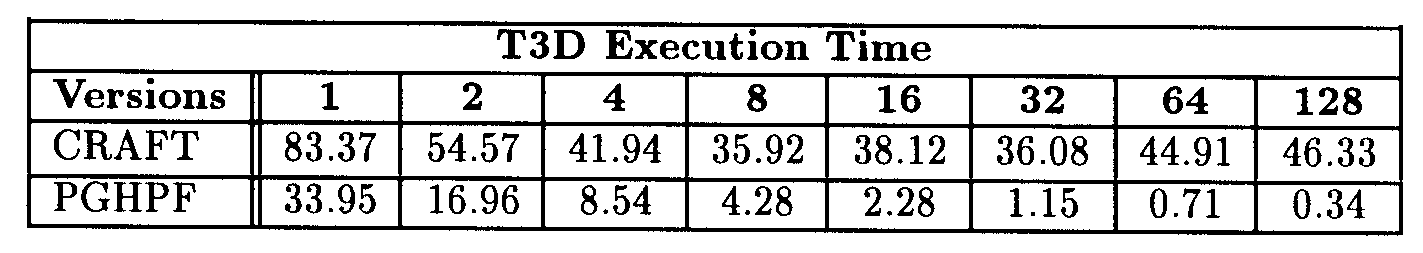
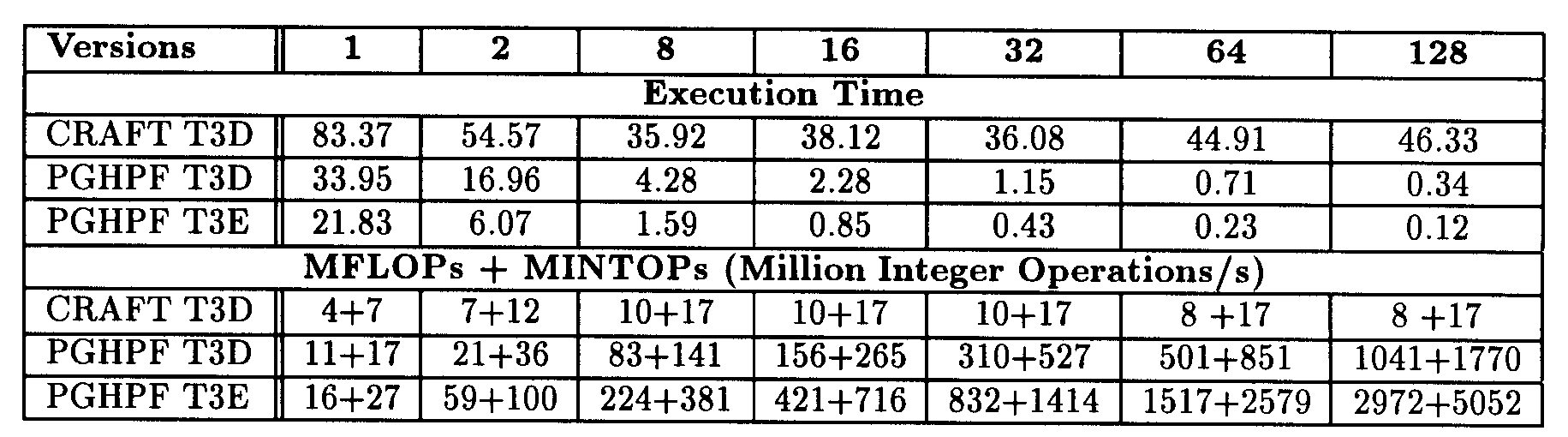
The Craft version achieved at best 10 MFLOPs plus 17 MINTOPs, on 32 processors. The good surprise was that the HPF version achieved good performanc as well as good scalability on T3D and T3E. Indeed, the HPF version aimed 8-10 MFLOPS + 14-17 MINTOPs/processor on T3D and 25-30 MFLOPS + 40-50 MINTOPs/processor on T3E until 128 processors.
Table 4
4 Tensrus: three-dimensional Tensor Product
Tensrus implements a three-dimensional tensor product. It is the kernel of a solver for elliptic differential equations (Poisson, Helmholtz..). The sequential version is due to Laurent Plagne CEA/DSM. It is applied to 64 x 64 x 64 to 512 x 512 x 512 matrices. It has been translated into HPF to Jean-Yves Berthou and Laurent Plagne. The main features of the method are described below:
- 3D domain with non-uniform Cartesian grid.
- B-spline collocation method of odd orders
- Multi-pole expansion is used to provide the boundary conditions
- The cost of the method is proportional to N4 (versus N3 log N for FFT) where N is the number of grid knots in one dimension. Nx,Ny,Nz can be different.
There is a large class of physical problems for which a non-uniform grid is a great advantage. In addition, because of the accuracy due to the use of B-spline, this method is, for certain problems, very competitive compared to FFT based ones2.
We have submitted Tensrus to the xhpf automatic parallelizer. xhpf produced in a few minutes a very inefficient code. By analyzing the resulting data parallel program, we understood that xhpf failed in generating the INDEPENDENT directives, that localize the parallel loops. These directives where placed in the innermost loops of the three loop nests that compose Tensrus, inducing a great amount of communication and a very small grain parallelism. Then, we corrected the HPF code generated by xhpf. This tooks us half a day. The three dimensional arrays manipulated by Tensrus are (BLOCK,*,*) or (*,*,BLOCK) distributed. The two dimensional arrays are replicated. Here is one of the three loop nests of Tensrus:
!HPF$ DISTRIBUTE (BLOCK,*,*) :: vect, fp, fpp
!HPFS DISTRIBUTE (*,*,BLOCK) :: te
CHPF$ INDEPENDENT
DO a = 1, nsx
DO b = 1, nsy
DO k = 1, nsz
fp(a, b, k) = O.O
DO c = 1, nsz
fp(a, b, k) = fp(a, b, k) + matz(k, c) * vect(a, b, c)
ENDO
ENDO
ENDO
ENDO
The three loops nests are parallel. All the communication are contained in the redistribution of the array fpp, which becomes (*,*,BLOCK) before the execution of the last loop nest. We also developped a MPI message passing version in 3 days. The following table summarizes the execution times, the efficiency of the parallelization of the HPF version and the MPI version of Tensrus executed on the Cray T3D. Tensrus is executed here on 64 x 64 x 64x matrices.
Table 5
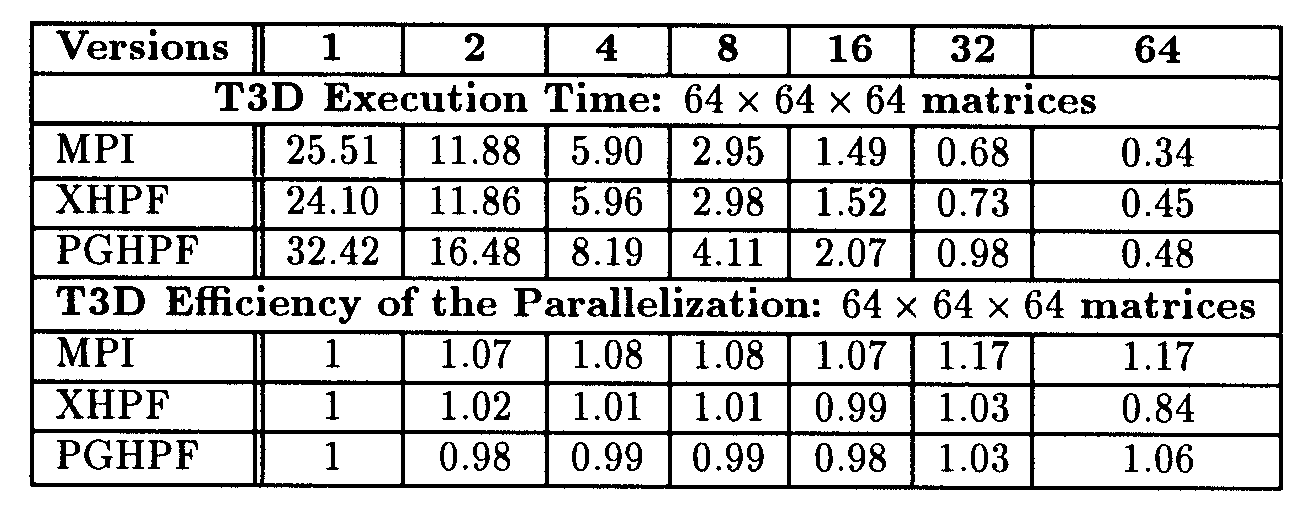
If xhpf is better than pghpf on a small number of processors, pghpf scales better. But above all, the efficiency of the HPF version is comparable to the one of the MPI version. Are we satisfied with these results? Absolutely not, since, if the efficiency is good, the performance is not good at all: 3.5 MFLOPs/PE. The parallel program has poor performance because the sequential source program is intrinsically inefficient. The main reason is that in Fortran the arrays are arranged in a column fashion while the arrays are accessed in Tensrus according to the rows. This leads to a very high number of cache misses during the execution. Thus, we applied numerous matrix transpositions in order to decrease the amount of memory accesses. But also in such a way that the outer loop of the three loop nests are parallel and the data distribution match the computation distribution. The sequential version of this new program, compiled by the Cray Fortran 90 compiler was much more efficient. We obtained 74 MFLOPs on T3D and 136 MFLOPs on T3E! We also submitted this new sequential version to xhpf which succeeded in producing the same HPF program we had hand coded. The performance of this code compiled by xhpf and pghpf on T3D and T3E are the following. The experiments have been conducted on 128 x 128 x 128 matrices:
T3D measures:
The HPF code compiled by xhpf leads to linear speed-up on 2 to 16 processors with 15 MFLOPs/PEs and 1.3 GFLOPs on 128 PEs. The HPF code compiled by pghpf leads to linear speed-up on 2 to 128 processors with 13 MFLOPs/PEs and 1.7 GFLOPs on 128 PEs.
T3E measures:
The HPF code compiled by xhpf leads to linear speed-up on 1 to 32 processors with 40 MFLOPs/PEs and 3.2 GFLOPs on 128 PEs. The HPF code compiled by pghpf leads to linear speed-up on 1 to 64 processors with 28 MFLOPs/PEs and 2.1 GFLOPs on 128 PEs.
We still observe that xhpf is better than pghpf with a small number of processors but pghpf scales better. We still were not satisfied by these results since the performance of the sequential version was four times better than the performance per processor of the HPF version. Then, we decided to gather the computations contained in the three loop nests of Tensrus (which are "local" computations) in PURE subroutines compiled separately with the Cray Fortran 90 native compiler. This new code transformation leads to the following version of the first loop nest. matmatl is the local computation performed by each processor.
!HPF$ DISTRIBUTE (*,*) :: matzt,matizy,matiizy
!HPF$ DISTRIBUTE (*,*,BLOCK) :: TE, fp, fpp
!HPFS DISTRIBUTE (BLOCK,*,*) :: vect
!HPF$ INDEPENDENT, NEW(matizy,matiizy)
do a=l,nsx
do b=l,nsy
do c=l,nsz
matizy(c,b)=vect(a,b,c)
end do
end do
call matmatl(matizy,matiizy,matzt,nsy,nsz)
do b=l,nsy
do k=l,nsz
fp(k,b,a)=matiizy(k,b)
end do
end do
end do
Since the xhpf compiler does not interpret the PURE clause, it can not compile this third HPF version of Tensrus. This version was the good one. We have executed the program for different matrix sizes: 128 x 128 x 128, 256 x 256 x 256 and 512 x 512 x 512.
Table 6
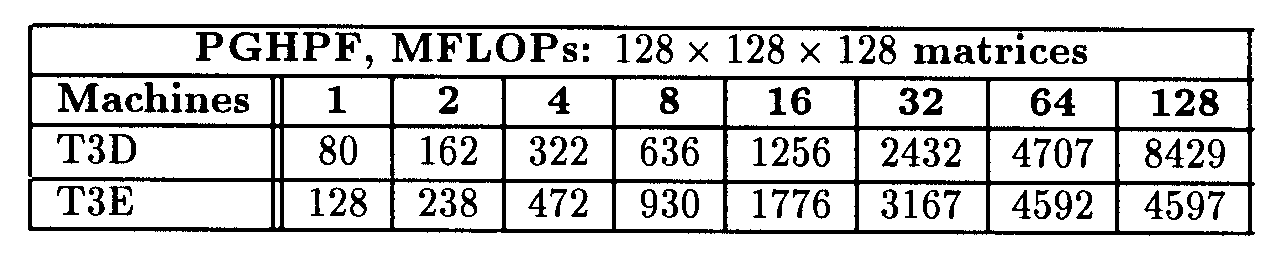
The performance on T3D is very good. Tenrus achieved 8.4 GFLOPS on 128 processors, that is 66 MFLOPs per processor. The performance on T3E decreases rapidly because there is not enough computation to feed the T3E processors. This is confirmed by the numbers we obtained on larger matrices:
Table 7
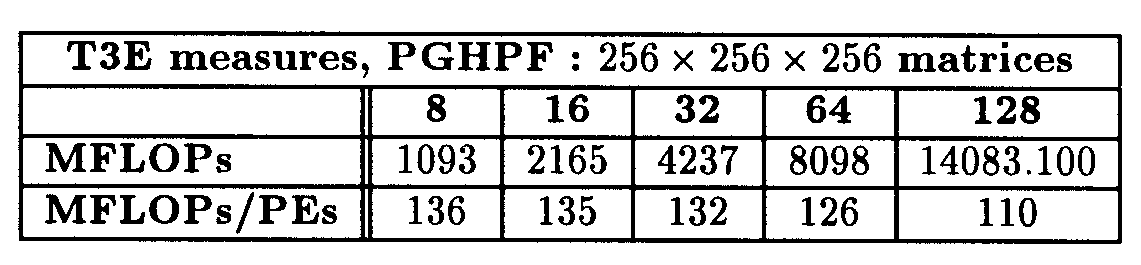
On 512 x 512 x 512 matrices, we obtained 19.5 GFLOPs on 128 PEs, which correspond to 152 MFLOPs per processor. On the new T3E configuration we received a few weeks ago, (PEs: 21164-375 Mhz, 256 PEs) we obtained 41 GFLOPs on 256 PEs, which correspond to 160 MFLOPs per processor.
5 Conclusions
The experiments conducted on the three codes shallow, Ising and Tensrus show that both automatic parallelization and HPF compilation may be efficient for the parallelization of scientific codes for parallel distributed memory machines.
First, these approaches are efficient for codes with static control which handle basic data structures (i.e. arrays) with linear access to memory.
Second, the parallelization of the shallow code shows that the rewriting of a sequential code in HPF may increase data locality. Such optimizations are efficient for distributed memory machines, shared memory machines, workstation networks, etc.
Third, automatic parallelization and HPF programming constitute the first steps towards the parallelization of intrinsically data parallel programs. Thus, even if the resulting parallel program proves inefficient, the time spent is paid off.
Finally, when automatic parallelization or HPF programming are efficient, they considerably speed up the production of parallel code. Moreover, HPF programming increases notably the maintenability of parallel code. Indeed, when Fortran 95 will be available, only one code will have to be maintain by the users: the sequential code plus HPF directives. This is not true with message passing programming, where two codes have to be maintained, the sequential source program and the parallel message passing version.
But things are not so rosy. Porting real applications written in HPF on MPP machines also revealed the current limitations of the xhpf and pghpf HPF compilers we used.
First, writing an efficient HPF code often means writing one "HPF" version for each HPF compiler. The first reason is that compilers do not interpret identically the HPF directives your HPF code contains. We should mention that the pghpf compiler interpretation of HPF directives is really close to the specifications of the HPF language, as defined by the HPF Forum. This is not true for the xhpf compiler. The second reason is that the efficiency of an HPF program may depend on the use of directives that are specific to the HPF compiler. This is a crucial point for xhpf, but it is less important for pghpf which has only added clauses to directives that will be partially included in the HPF 2.0 approved extensions. The third reason is that compilers do not accept the same subset of the Fortran 90 language. Again, this is currently a real problem for xhpf, not so much for pghpf. Accepting the whole Fortran 90 language in the near future is the number one priority of Applied Parallel Research and Portland Group Inc.
Second, as shown with the parallelization of the Tensrus program, the more you hide to the HPF compiler, the more the parallel code is efficient. More precisely, the larger is the part of the source code compiled by the native Fortran 90 compiler, the better is the performance of the parallel code. This also means that local computations have to be performed as much as possible using routines of sequential libraries (i.e, Benchlib, scilib on Cray MPP machines). The parallelization of Ising showed that the HPF compilers, and especially pghpf, efficiently compile INTRINSICS subroutines.
Third, it might happen that the performance of the parallel generated code is actually worse than the performance of the sequential code. A fragment of code whose execution time is negligible may become a very consuming time fragment in the HPF version. For example, this is the case when the compiler applies the run time resolution. Thus, porting a large application is hazardous. Under HPF2.0 it will be possible for the user to put these fragments of code into HPF_SERIAL extrinsic procedures. Such procedures are guaranted to be executed on one processor. This eliminates the communication and computation overhead induced by the run time resolution.
Fourth, the learning effort for good HPF coding is substantial. Users must know Fortran 90 (and Fortran 95 in the near future), HPF features and the compiler-specific characteristics in order to obtain good performance.
Fifth, HPF directives are only advice the user gives to the compiler. The compiler may follow them or not. Moreover, the user does not necessary specify the mapping of the data on the physical processors of the target machine, or the alignement between arrays. This implies that the compiler has to make some choice about the data mapping, the data alignement and sometimes about the data distribution. It is absolutely necessary that compilers specify, as xhpf does partially, the choices done. Without this information the user has great difficulties in understanding the work the compiler does and then, great difficulties in debugging or improving its HPF code.
To conclude we think that the HPF compilers should improve their portability. This means they should compile the whole Fortran 90 language and the whole HPF langage. They should also interpret the HPF directives as specified by the HPF language specifications (a bad example is the way xhpf manages dummy argument distribution). Their efficiency must not depend on compiler-specific directives. They should provide tools adapted to data parallel programming such as visualization tools for distributed data structures like HPF-Builder from LIFL Lille University[LD96, LD97]. For instance, if an application performs computations on several three-dimensional arrays, it is not easy for the user to take into account the different possibilities of distribution along each dimension (or alignement and mapping) in order to improve the efficiency of the loop nest associated to these arrays.
Endnotes
1 The efficiency of the parallel program E(p) is equal to E(p) = Tl/pTp, where p is the number of processors, T1 is the execution time of the sequential program and Tp is the execution time of the parallel program executed on p processors. This quantity measures the absolute gain in performance of the parallel program.
2 For more information, please contact Laurent Plagne, plagne@drfmc.ceng.cea.fr
References
[BMN+97] Z. Bozkus, L. Meadows, S. Nakamoto, V. Schuster, and M. Young. Pghpf - an optimizing high performance fortran compiler for distributed memory machines. Scientific Programming, 6(1):29-40, Spring 1997.
[CCM95] C. Calvin, L. Colombet, and P. Michallon. Overlapping Techniques of Communications. In Proceedings of HPCN'95, Mai 1995.
[Fea93] Paul Feautrier. Toward automatic partitioning of arrays on distributed memory computers. In ACM ICS'93, pages 175-184, Tokyo, Juillet 1993.
[For94] High Performance Fortran Forum. High Performance Fortran Language Specification, version 1.1. Technical report, Center for Research on Parallel Computation, Rice University, Houston, TX, Novembre 1994.
[Ger90] M. Gerndt. Updating distributed variables in local computations. In Concurrency: Pratice & Experience, pages 2(3):171-193, Septembre 1990.
[LD96] Christain Lefebvre and Jean-Luc Dekeyser. Hpf-builder: A visual environment to transform fortran90 codes to hpf. In J. J. Dongarra and B. Tourancheau, editors, Third Workshop on Environments and Tools for Parallel Scientific Computing, August 1996.
[LD97] Christain Lefebvre and Jean-Luc Dekeyser. Hpf-builder: Visual hpf directives programming environment. In High Performance Fortran(HPF) User Group, February 1997.
[Res95] Applied Parallel Research. Forge high performance fortran, xhpf version 2.1, user's guide. Technical report, Octobre 1995.
[TPG96] Inc The Portland Group. pghpf user's guide, version 2.1. Technical report, Mai 1996.