Miltos D. Grammatikakis, Helidon Dollani, and Stefan Liesche
{mdgramma,dollani,liesche}@informatik.uni-hildesheim.de
http://www.informatik.uni-hildesheim.de/~mdgramma
In low-level (virtual) shared memory programming, processors can access local and remote memory using read, write, and atomic operations. Synchronization is needed to avoid data consistency problems, called race conditions [14]. Data races arise when threads or parallel processes access shared variables and
Synchronization routines can be classified into either blocking or busy-wait. While with blocking waiting processes are deferred, thereby freeing the CPU to perform other operations, with busy-wait processes repeatedly access shared variables to determine when they may proceed. Busy-wait synchronization is a better approach when scheduling overhead exceeds busy-wait time, when CPU resources are not needed by other threads, or when rescheduling is inappropriate, as in a single-user system.
Busy-wait synchronization includes acquire_lock and release_lock mechanisms for mutual exclusion, post and wait semaphores for producer-consumer problems, and non-fuzzy barriers for bulk-synchronous computations [11]. Although hardware barriers are now common in most NUMA supercomputers, such as the TMC/CM-5 and Cray-T3D/T3E, Fujitsu and Hitachi MPP systems, locks and special semaphores (condition variables) are generally implemented using library calls. A lock is more restrictive than a semaphore. Not only it is a binary object, but also a release lock operation can only be performed by the last processor to acquire the lock. Performance of these synchronization operations benefits from the availability of hardware supported atomic operations, such as Test&Set, Fetch&Increment, Fetch&Add, Fetch&Store, Compare&Swap, and Load_Linked/Store_Conditional [13].
Two of the most important and widely used busy-wait synchronization mechanisms are spin locks, and (non-fuzzy) barriers. Spin locks provide means for implementing mutual exclusion and avoiding data races. They ensure that only one processor may access (and possibly modify) a shared data structure at any given time. Spin locks protect application critical sections, and may be executed an enormous number of times with concurrent data structures, such as priority queues, FIFO queues, e.g. in OS kernel processing routines, or fault tolerance recovery techniques. Apart from concurrent implementations of linked lists and sometimes queues which can be done in a lock-free fashion, locks are generally needed in most asynchronous implementations of shared memory algorithms, e.g. a concurrent implementation of a Gaussian solver of A X =B. Barriers provide mechanisms for ensuring that no process advances beyond a particular point in computation until all processes have arrived at that point. Barriers are also used for avoiding race conditions, and may be a major contributor to run time.
A concurrent algorithm is said to be lock free if it always guarantees that some process will complete in a finite number of steps. It is wait free if it guarantees that each process will complete in a finite number of steps. A hierarchy of atomic principles enabling the simulation of lower class primitives in a wait free manner has been developed [7]. The hierarchy leads to interesting emulations of atomic operations and higher level synchronization principles.
In this paper we examine several implementations of locks on Cray-T3E virtual shared memory systems. In Section 2, we discuss the implementation of spin locks, including Test&Set-based lock, Ticket Lock, Anderson's Lock, and Mellor-Crummey and Scott (MCS) Lock for virtual shared memory. In Section 3 we evaluate spin locks, by computing the average time for acquire and release lock operations. We concentrate on both small, and large critical sections. We show that Anderson's and MCS Lock minimize network contention, and offer improved performance over all other locks for any system with more than two processors. In fact, MCS Lock is 1000 to 10,000 times faster than the Cray-T3E shmem_test_lock & shmem_set_lock instructions for 64 processors.
Nowadays most non-uniform memory access (NUMA) supercomputers, including Cray-T3E, NEC SX-4, and to a lesser degree Hitachi SR-2201 and Fujitsu VPP700, support virtual shared memory (VSM).
The Cray-T3E implements a logically shared address space over physically distributed memories (with up to 2GB per processor). Each processing element (PE) consists of a DEC Alpha 21164 processor connected to a "shell", consisting of a control chip, a router chip and local memory. The T3E improves the memory bandwidth of the Alpha microprocessor by providing a large set (512 user plus 128 system) of external registers (called E-registers). These registers are used to support remote communications and synchronization. Because of the large number of E-registers, remote reads and writes are highly pipelined. The operations that read memory into E-registers and write E-registers to memory are called respectively, shmem_get and shmem_put. On the Cray-T3E both operations have similar performance. However, due to adaptive packet routing, successive calls to shmem_put are not guaranteed to arrive in order. Special calls to shmem_quiet/shmem_fence are needed to verify that all previous puts from/to a particular PE have executed in order.
On the Alpha microprocessor a Load_Linked/Store_Conditional implements an atomic read-modify-write cycle; this is the only atomic operation available consistent with its RISC philosophy [3]. The Load_Linked(a) primitive returns the value M(a) and sets a reservation associated with the location and the processor (but does not lock the location). A subsequent Store_Conditional(a,b) instruction checks the reservation, and either succeeds writing the value of b, if the value at that location has not been modified, or otherwise it fails.
The Cray-T3E provides a plethora of atomic operations on arbitrary memory locations, allowing an unlimited number of synchronization variables. The atomic operations provided by the Cray-T3E are Fetch&Inc, Fetch&Add, Compare&Swap and (masked) Swap. Notice that Fetch&Store, Compare&Swap, or Load_Linked/Store_Conditional can be used to implement Test&Set, hence Test&Set is not provided in most modern MPP systems, like the Cray-T3E.
Atomic operations on the the Cray-T3E are implemented using the Alpha microprocessor's Load_Linked/-Store_Conditional/Store_Conditional primitive. The main idea of these implementations is to repeatedly execute Load_Linked/Store_Conditional cycles, until the Store_Conditional is successful, thus the operation appears to be atomic since there is no overlapping with other operations accessing the same memory location. In practice Load_Linked/Store_Conditional checks a complete cache line.
Barriers allow a set of participating processors to determine when all processors have signaled some event (typically reached a certain point in their execution of a program). Barriers are implemented in hardware on the Cray-T3E using combining trees.
Cache coherence is implemented on the Cray-T3E using cache-invalidate protocols. However, the T3E is not stream coherent and prefetching must be turned off to avoid data race conditions which may cause inconsistent results, program aborts, or hangs. It is also known that the T3E may reorder instructions from a given PE, e.g. local remote writes and remote read operations (WR reorder). A released consistency model has been proposed based on the Alpha microprocessor [3].
Atomic operations are supported on all Cray MPP and PVP systems by calling Cray ShMem library functions. ShMem library calls can be used within Fortran and C/C++ programs. Since our implementations are in C only C/C++ routines are presented.
Atomic operations available to users and operating system programmers on the Cray-T3E are shown in Table 1. The operands are generally short (32-bit) integers; some operations allow also for other data types, such as int, long, float, and double. A definition of each operation listed in Table 1 is provided below:
1) Fetch_(a,b) operations return the memory contents M(a),
while storing at location a the function
.
2) Compare&Swap(a,b,c) primitives atomically compare the content of memory location M(a) with a replacement value b, and store a third value c if they match; the operation also returns a condition flag indicating either success, or failure.
3) (masked) Swap(a,b,c) operations store selected bits from c in M(a). Selection is done by the mask b. It returns the previous content of M(a).
4) acquire_lock/release_lock(a) routines together provide mutual exclusion. The first call to acquire_lock(a) returns immediately. A successive call returns after a release_lock(a) corresponding to the first acquire_lock(a) is executed. This ensures that only one process is holding the lock at a time.
Also notice, that due to adaptive routing of messages, successive calls to shmem_put are not guaranteed to arrive in order. Special calls to shmem_quiet (shmem_fence) are needed to verify that all previous puts from (to) a particular PE have executed in order.
In this Section, we describe five implementations of a mutual exclusion spin lock. In our busy-wait lock implementations, processors call acquire_lock whenever they desire a lock (there are no synchronization barriers involved). Acquire_lock will return only when the lock is obtained by the calling processor. A subsequent call to release_lock will make the lock available to other competing processors.
Each algorithm assumes a virtual shared memory environment that allows for atomic, remote write, and remote read operations. In our presentation, we will use the macro names: fast_finc, fadd, cswap, and swap referring to atomic operations as shown in Table 1. Furthermore, most of our lock variables will be of type short; this entails no severe limitation of the use of our routines and faster remote operations are possible.
The simplest mutual exclusion lock employs a polling loop to access a boolean flag that indicates whether the lock is held. As the C code in Table 2 indicates, in acquire_lock each processor repeatedly executes a Test&Set operation (via a swap) in its attempt to change the flag from false to true. The processor will then release the lock by setting the flag back to false. The main shortcoming of the Test&Set Lock is network contention for the flag, which is allocated at a given PE (usually PE0).
The total amount of network traffic caused by busy-waiting on a Test&Set Lock can be reduced by introducing a random delay at each processor between consecutive probes of the lock. The simplest method employs a constant delay; more efficient schemes adopt exponential backoff on unsuccessful probes [1]. This is also shown in Table 2.
In Test&Set Lock, the number of read-modify-write operations is potentially large, and each Test&Set operation would cause invalidation of all cache copies on a cache coherent system. Although every waiting processor may perform a Test&Set operation on the same flag each time, only one will actually acquire the lock. We can reduce remote cache invalidations (and possibly network traffic) using a Ticket Lock, while at the same time we ensure FIFO service; i.e. granting the lock to processors in the order that they request for it.
A Ticket Lock consists of two counters. The request counter Ticket counts the processors that call acquire_lock, while the release counter Serve counts the times the lock has been released. A processor acquires the lock by performing
It releases the lock by
Our implementation of Ticket Lock on the Cray-T3E is shown in Table 3.
Ticket Lock causes substantial memory and network contention by polling a common location. As with Test&Set Lock, this contention can be reduced by introducing delay on each processor between consecutive probes of the lock. In this case however, exponential backoff is not a good idea. Instead proportional backoff is implemented, and the delay is made proportional to the difference between the values of the request and release counter. The constant of proportionality is the minimum time that a processor can hold the lock [11].
Even for Ticket Lock with proportional backoff, it is not possible to obtain an average constant number of network transactions per lock acquisition, due to the unpredictability of the length of critical sections. Anderson has proposed a locking algorithm that achieves constant network traffic on cache coherent shared memory multiprocessors that support Fetch&Increment (or Fetch&Store) operations [1]. Expanding on Anderson's idea to virtual shared memory systems, the trick is that each processor uses an atomic swap to save its address at the PE named Ticket. Then processors performing release_lock can directly inform the next processor to acquire the lock, by writing directly on its spinning variable my_flag.
This idea is implemented on the Cray-T3E as shown in Table 4. Notice that, each processor spins on its local variable which can be arranged to be on a different cache line. The Fetch&Increment in Anderson's algorithm could also be avoided by using a single Fetch&Store operation (on the corresponding subfields) [6].
The MCS Lock, as prototyped by Mellor-Crummey and Scott, guarantees FIFO ordering of lock acquisitions, spins on local variables only, requires a small constant amount of space per lock, and works equally well on machines with and without coherent caches. We have adjusted the MCS Lock to the virtual shared memory model. The resulting code for the Cray-T3E appears in Table 5.
A Lock variable is allocated at processor 0. Its contents are either null (-1) if the lock is still available, or otherwise set equal to PE, if processor PE has acquired the lock. Each processor using the lock must allocate two queue pointers (predecessor and next) and a boolean flag (my_flag). The predecessor variable points to the previous processor requesting an acquire_lock, or is null if no PE has done so. The predecessor variable is used to notify the predecessor PE by setting its local variable next; this variable is initialized to -1 in acquire_lock. A processor issuing an acquire_lock either obtains the Lock, or spins on its local my_flag, until the Lock becomes free.
On a release_lock operation the queue pointer next is checked. If next is non-empty we pass the Lock to the next PE by setting the corresponding my_flag variable. If next is empty, a Compare&Swap enables the processor to determine whether it is the only processor in the queue. In this case, the processor simply resets Lock to -1, in a single atomic action. Otherwise, there is another processor waiting for the Lock, so we wait until this other processor sets the next pointer of this PE, so that we can inform him. This local spin in release_lock compensates for the time window between the Fetch&Store (swap) on Lock and the later assignment to next in acquire_lock.
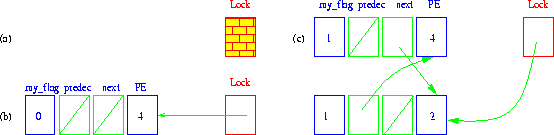 |
Chains of processors holding and waiting for the lock are shown in Figure 1. In
Upon releasing the lock PE4 will notify the next processor (PE2) using a remote write on its my_flag variable. Notice the corresponding next and predecessor queue pointers.
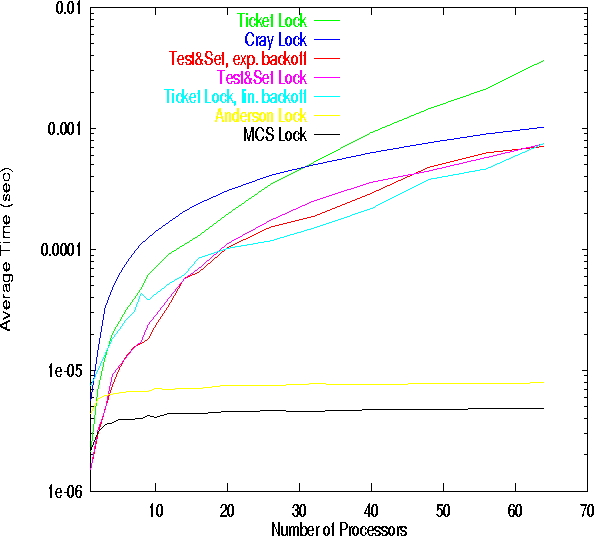 |
We now evaluate the average time each processor spends on acquire_lock and release_lock operations. The time spent in the two routines on the Cray-T3E900 is added together. In Figure 2 we show the performance for a small synthetic critical section. For any number of processors P> 2, Anderson and MCS lock are far superior to any choice of Test&Set or Ticket Lock. If only one or two processors are requesting a lock, and FIFO ordering of lock requests is not important, then a simple Test&Set is the best choice. This is also true when lock is an extremely rare operation; however, in this situation, one can argue that a lock may be dropped without introducing race conditions. Furthermore, the performance of Test&Set with exponential backoff is only slightly better than Test&Set with no backoff. For Ticket Lock we have found proportional backoff to be generally a bad idea, especially for large critical sections.
The Cray lock, probably implemented as a Ticket Lock, since it guarantees FIFO ordering (and analysis of the assembly code indicates that PEs access a variable at a fixed PE), is extremely slow. It is, including runtime lock validation, between 1000 to 10,000 times slower than MCS Lock for 64 processors! This would be several orders of magnitude slower on a full-scale Cray-T3E system.
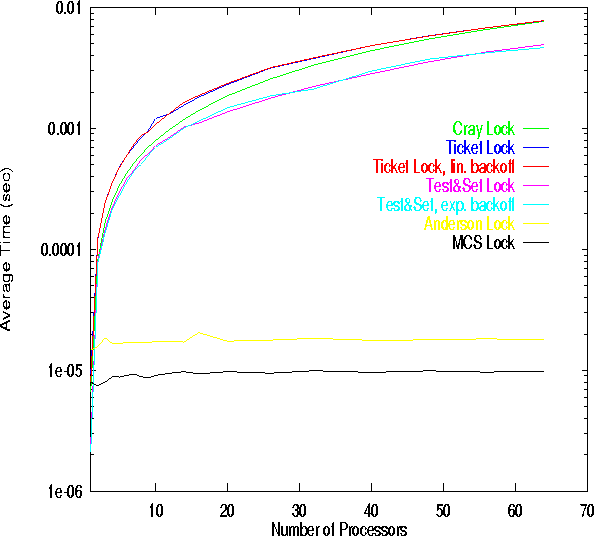 |
Similar results for large critical sections, shown in Figure
3, verify the above observations. In this case, the critical section consists
of a loop with 1 million integer operations; large critical section, refers to the average
time spent in the loop compared with the minimum time taken by an acquire_lock
together with a release_lock operation.
The performance of locks is of a great importance to several problems which lie in the heart of concurrent data structures, operating systems, and fault tolerance. Our implementations of Anderson's Lock and MCS Lock minimize internetwork and memory traffic and achieve performance at levels of several orders of magnitude better than Test&Set Lock, Ticket Lock, or Cray-T3E library shmem_lock implementations.
In several applications, alike Ticket Lock and Anderson's Lock, there is access
to centralized counter. Implementing this counter as a counting network
can reduce bottlenecks. Counting networks provide a distributed mechanism
for implementing Fetch&Increment, by avoiding the traffic associated with accessing
a single (virtual) shared memory location [2]. Implementation
of fan-in two, -depth counting networks, isomorphic to Batcher's bitonic sorting network [4], or the balanced periodic sorting network [5],
shows the practicality of this low-level approach [8].
Implementations of other synchronization issues, such as software barriers on
the Cray T3E are interesting. For non-fuzzy barriers, we do not expect improvements,
since Cray-T3E hardware barriers have almost constant runtime (), independent
of the number of PEs (N). This is always faster than a software barrier, whose
runtime depends on the number of PEs participating in the barrier [11],
usually as
. However, fuzzy nonblocking barriers are interesting and their implementation
could be useful for optimizing certain latency-bound applications.
We currently consider the effect of our lock implementations on parallel network
simulation algorithms by implementing concurrent priority queues using atomic operations [12,9]. These data structures support priority
insert and delete min operations which are necessary for modeling network
packet movements. Since, 20-30% of our parallel code consists of calls to lock operations,
we claim that our analysis (which will be included in the final version of this paper)
will make our results even stronger [10]. We hope that improved
lock/semaphore implementations in NUMA supercomputers would encourage programmers
to consider concurrent, shared memory data abstraction for high performance applications.
We acknowledge partial support from KFA, Jülich - project INTENS. This work was performed while the second author was visiting from the Department of Mathematics, University of Tirana, Tirana, Albania, supported by a DAAD short-term research scholarship (A/97/12720). The last author was partially supported by EPCC/TRACS through an HCM scholarship. We are greatful to Prof. Michael Scott for his helpful comments.