Witold Rudnicki, Rafal Maszkowski, Lukasz Bolikowski, Maciej Cytowski, Maciej Dobrzynski, Maria Fronczak
Interdisciplinary Center of Mathematical
and Computational Modeling,
Warsaw University
May 2006
ABSTRACT: We have implemented a parallel version of Position-Specific Iterated Smith-Waterman algorithm using UPC. The core Smith-Waterman implementation is vectorized for Cray X1E, but it is possible to use an FPGA core instead. The quality of results and performance are discussed.
KEYWORDS:
Cray X1E, UPC, bioinformatics, Smith-Waterman, sequence alignment
This paper in PDF format.
The aim of this paper is to briefly summarize some technical aspects of implementing the Position-Specific Iterated Smith-Waterman algorithm for local sequence alignment on Cray architecture.
The project was initiated at the Interdisciplinary Center of Modeling in 2002. At first, our goal was to test the capabilities of the BMM unit1by implementing the original Smith-Waterman algoritm on Cray SV1. At that time there was no BioLib2package, nevertheless an equivalent tool was necessary. It turned out that the Smith-Waterman algoritm itself cannot substantially benefit from the BMM, but a better understanding of the unit allowed us to design certain filters that would limit the number of calls to the S-W routine. This work was presented by Lukasz Bolikowski on CUG 2005 conference in Albuquerqe.
Finally, as Cray X1 appeared at ICM, it was feasible to implement the iterated version of S-W (PSI S-W), in a fashion similar to the PSI BLAST3. It was tempting to check whether such approach could be competitive to PSI BLAST in terms of speed, and whether the alignments obtained by PSI S-W could be substantially better than ones obtained by PSI BLAST. We have parallelized our code with UPC4
The purpose of Smith-Waterman algorithm is to find a local alignment of two sequences that is maximal according to the chosen scoring system.
The sequences are simply strings of letters: there are 20 letters to choose from
in case of amino acids and 4 letters in case of nucleotides.
Let us explain what a local alignment is by an example.
Take two amino acid sequences:
MDRKVTPGSTCAVFGLGGVGLSAIMGFIL
and
MKLNPGSSGHGGMGATMTSAVMGDRNN.
The optimal local alignment for the two is:
Query: 4 KVTPGSTCAVFGLGGVG---LSAIMG 26
K+ PGS+ G GG+G SA+MG
Sbjct: 2 KLNPGSS----GHGGMGATMTSAVMG 23
The top row is a fragment of the first sequence, the bottom row is a fragment of the second one. Each letter of a sequence is assigned to a letter in the other sequence, or to a gap between two consecutive letters in the other sequence.
A scoring system for all alignments shall be defined to select the optimal alignment from the set of all possibilities. The system used by the Smith-Waterman algorithm is based on the probability of various mutations, such as replacements, insertions and deletions, in the protein sequences.
The score of an alignment is computed as follows:
each aligned pair of letters is given an integer
value, and the values are summed up. Then each
gap of length ![]() is given a penalty
is given a penalty ![]() ,
where
,
where ![]() and
and ![]() are constants named gap opening penalty
and gap extension penalty.
Finally, all the penalties are substracted from the sum
and the result is the alignment score.
are constants named gap opening penalty
and gap extension penalty.
Finally, all the penalties are substracted from the sum
and the result is the alignment score.
The scoring system is, thus, respresented by a symmetric
table ![]() of scores for each pair of letters, and a pair
of scores for each pair of letters, and a pair
![]() of penalties. The table is
of penalties. The table is ![]() for
amino acids and
for
amino acids and ![]() for nucleotides. A fragment
of BLOSUM62, a popular amino acid scoring table, is shown below:
for nucleotides. A fragment
of BLOSUM62, a popular amino acid scoring table, is shown below:
| A | R | N | D | C | Q | E | |
| A | 4 | -1 | -2 | -2 | 0 | -1 | -1 |
| R | -1 | 5 | 0 | -2 | -3 | 1 | 0 |
| N | -2 | 0 | 6 | 1 | -3 | 0 | 0 |
| D | -2 | -2 | 1 | 6 | -3 | 0 | 2 |
| C | 0 | -3 | -3 | -3 | 9 | -3 | -4 |
| Q | -1 | 1 | 0 | 0 | -3 | 5 | 2 |
| E | -1 | 0 | 0 | 2 | -4 | 2 | 5 |
Note that the diagonal elements are always positive and
greater than any other one in the row.
This is natural, since alignment of a sequence ![]() with
itself (a perfect alignment) should have score greater
than any alignment of
with
itself (a perfect alignment) should have score greater
than any alignment of ![]() with a different sequence.
with a different sequence.
The Smith-Waterman is a simple dynamic programming algorithm.
Let ![]() and
and ![]() be the two sequences being aligned. It starts by
allocating a table
be the two sequences being aligned. It starts by
allocating a table ![]() of dimensions equal to the lengths of
of dimensions equal to the lengths of ![]() and
and ![]() .
Then it fills the table from upper-left to bottom-right (by rows, columns
or antidiagonals - any of these orders is good) with value:
.
Then it fills the table from upper-left to bottom-right (by rows, columns
or antidiagonals - any of these orders is good) with value:
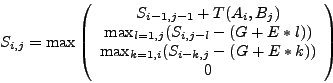 |
(1) |
![]() and
and ![]() here stands for gap penalties:
here stands for gap penalties: ![]() when a gap is opened and
when a gap is opened and ![]() , when it
is extended. The intuitive meaning of a value
, when it
is extended. The intuitive meaning of a value ![]() is the score of the best
local alignment ending at
is the score of the best
local alignment ending at ![]() .
.
At each step, when a maximum value is found, it should be recorded from which
direction the result was obtained: diagonal, top, left, or none.
The table ![]() together with information about the directions provide
enough data to find the best local alignment.
together with information about the directions provide
enough data to find the best local alignment.
To find the best alignment, one has to do as follows.
First, find the maximum value within table ![]() .
This is the end of the highest scoring local alignment.
Then, backtrace from the cell in the recorded direction.
A diagonal move from
.
This is the end of the highest scoring local alignment.
Then, backtrace from the cell in the recorded direction.
A diagonal move from ![]() to
to ![]() represents
an aligned letter pair
represents
an aligned letter pair ![]() ;
a horizontal move from
;
a horizontal move from ![]() to
to ![]() represents
represents
![]() aligned with a gap between
aligned with a gap between ![]() and
and ![]() ;
a vertical move is analogous to the horizontal one;
while
;
a vertical move is analogous to the horizontal one;
while ![]() at
at ![]() means the optimal local alignment
starts at
means the optimal local alignment
starts at ![]() .
.
A typical use of a local alignment algorithm is such: one sequence, a query, is aligned against a database of sequences, one by one. The most significant alignments, and their corresponding sequences are presented to the user.
Position Specific Iterated Smith Waterman (PSI-SW) is an extension of the original SW algorithm analogous to the PSI-BLAST extension of the BLAST algorithm. In this algorithm the single scoring table is replaced by the position specific scoring matrix (PSSM or profile). A set of unique 20 scores for each amino acid in the query sequence is used. These scores are obtained in the iterative self-consistent procedure. In the first step the scores from the similarity matrix, such as BLOSUM62 are used to find the set of homologous sequences. Then all sequences are aligned with the query and frequencies of the aminoacid appearance at each position is computed and translated into the scores in the position specific scoring matrix. Then a new search for the homologous sequences is performed using new PSSM, presumably leading to finding more homologous sequences than in the search with the original socring matrix. This procedure is repeated until no more new sequences are found.
The core Smith-Waterman algorithm is quite straightforward
to implement. One crucial observation is that updating the
![]() table should be done by antidiagonals, since all operations
on a antidiagonal are then independent of each other, which
enables vectorization.
table should be done by antidiagonals, since all operations
on a antidiagonal are then independent of each other, which
enables vectorization.
The implementation of PSI S-W algorithm was also straightforward. It required certain changes to the original S-W code, since the iterated version introduces Position-Specific Scoring Matrices (PSSM) instead of the traditional scoring tables.
There are two possible bottlenecks in the parallel implementation of
the algorithm. First is a possible load inbalance due to the
unbalanced database split.
We applied the following procedure to minimize this inbalance:
All proteins in the database were sorted with respect to
their lenght. Then, starting with the shortest sequences we put each
sequence one by one into actually smallest set. Note that usually one
compares sequences to some well known databases which can be split
into ![]() parts in advance.
parts in advance.
Another possible bottleneck arises due to the application of the
parallel library in the implementation. The library enforces
co-ordination between processors, which may slow down the execution,
when proteins of different lengths are executed on different CPU's.
Nevertheless we decided to use the parallel library, because
we need to collect the results from each processor after each
single iteration in order to compute a new position specific matrix.
Such a matrix is than used as a substitution matrix in next
iteration.
The UPC was used, because it is user friendly parallel library,
which is also well suited for the CrayX1E architecture.
We have implemented two S-W procedures: one which finds the maximum score and one which performs full S-W algorithm including the path reconstruction step. Each time we run the first fast procedure to check if E-value of the best alignment is better than preset threshold. If it does, the full S-W procedure is called. On average this implementation is 50% faster than full S-W procedure.
The tool output is similar to the reports generated by BLAST for at least two important reasons: the reports are easy to read, and is familiar for most potential users.
An important step in selecting the alignments that are to be reported to the user is to assess their statistical significance. The tool assesses the significance using Karlin-Altschul-Dembo theory, the same that is used by BLAST ([4], [5]).
We have performed the test using the SCOP classification of the protein domains. We checked sensitivity of the searches, for all proteins from PDB with similarity lower than 98%. We compared results of PSI BLAST and PSI S-W algorithms.
The preliminary results suggest, that for identical parameters for the PSI procedure, the PSI SW has slightly higher sensitivity, but lower specificity. The testing procedure is under way and results will be reported elsewhere.
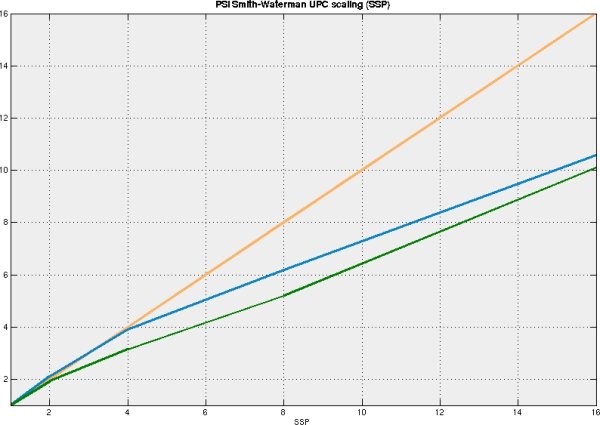
The Smith-Waterman algorithm has been implemented on X1 architecture, independently from the implementation included in Cray BioLib, with similar performance. The parallel UPC version of the program has been implemented, and reasonable parallel scaling has been achieved. The performance of the code on the vector architecture is significantly higher than on the PC, neverthless it is still at least order of magnitude slower than that of PSI-BLAST - the standard tool used for homology searches. Implementation of SW core algorithm to the FPGA architecture is underway in our laboratory, which might have performance comparable to current implementations of BLAST.
Sensitivity and specificity of the PSI S-W has been compared with PSI BLAST, with PSI S-W displaying slightly higher sensitivity and PSI BLAST displaying higher specificity, for the same set of PSI parameters.
The project was led by Dr.Witold Rudnicki, Deputy Director, HPC Division, ICM. His scientific research focuses on bioinformatics and HPC. He can be reached at: ICM Warsaw University, Pawinskiego 5A blok D, 02-106 Warsaw, Poland, e-mail: rudnicki@icm.edu.pl. Lukasz Bolikowski, Maciej Cytowski, Maria Fronczak and Rafal Maszkowski are Software Developers at ICM. Maciej Dobrzynski was a student of Dr.Rudnicki in an early stage of the project.
A large portion of work was done by Witold Rudnicki and Rafal Maszkowski, who initiated the project. Witold was responsible for the theoretical design, while Rafal implemented the core S-W.